데이터 축소
데이터 축소 특징
•
방대한 양의 데이터를 분석하기 위해서는 많은 시간이 소요됨
•
실용적이지 못하거나 분석이 불가능할 수도 있음
•
원본 데이터에 가까운 품질을 유지하면서 축소된 데이터 셋을 확보하는 것이 필요함
•
데이터 저장 및 분석 비용을 줄임
도메인 지식 기반 차원 축소 방법
•
속성 하위 집합 선택
•
관련성이 없고 중복된 기능이 있는 경우에는 정보의 손실이 발생하지 않음
중복 속성 제거
•
관련 없는 속성 제거
◦
예) ‘지불한 금액’ , ‘제품 구매 가격’
•
해결하고자 하는 문제에 중요한 정보를 포함하지 않는 속성을 제거
◦
예) 학생의 성적을 예측해야 하는 작업에서 학생의 ‘학번’ 속성
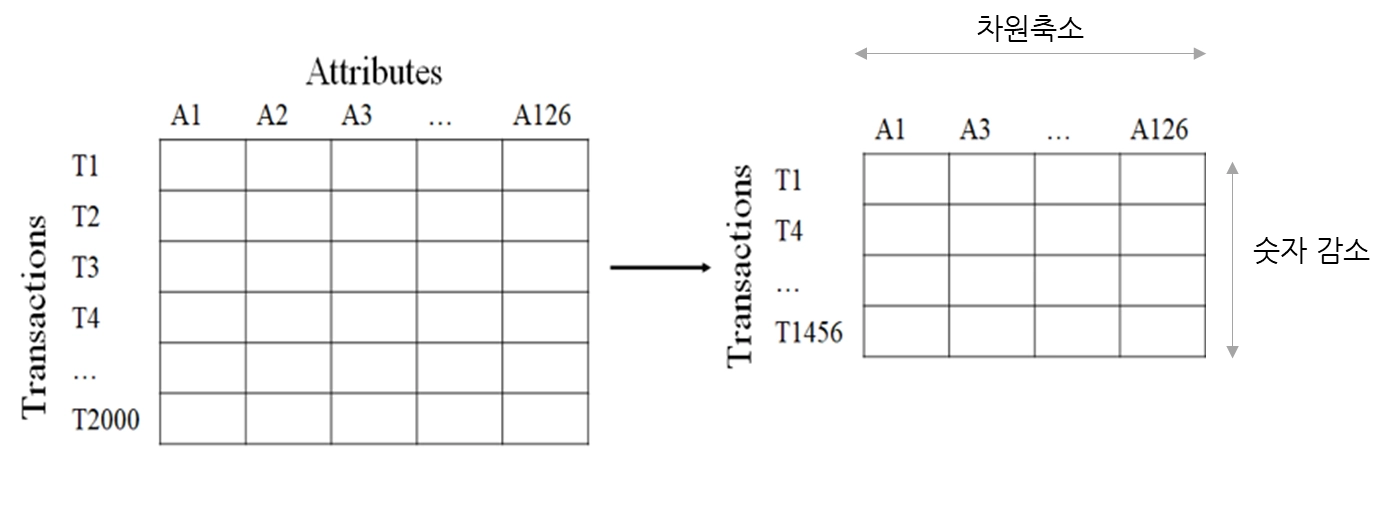
데이터 축소 방법
차원축소 vs 인스턴스 축소(숫자 감소)
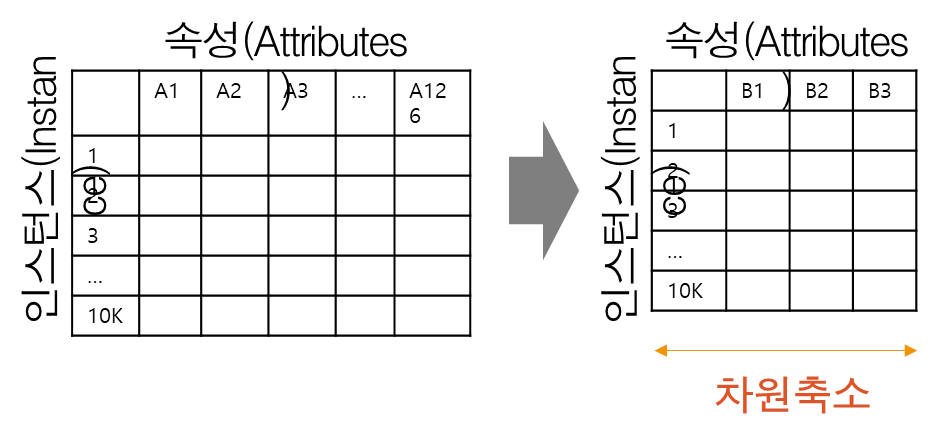
차원 축소(Dimension Reduction)
•
속성(feature) 선택 또는 속성 하위 집합 선택
•
데이터 분석 시, 관련성이 적거나 중복되는 속성을 찾아 제거함
•
매우 많은 피처로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성
차원 축소의 필요성
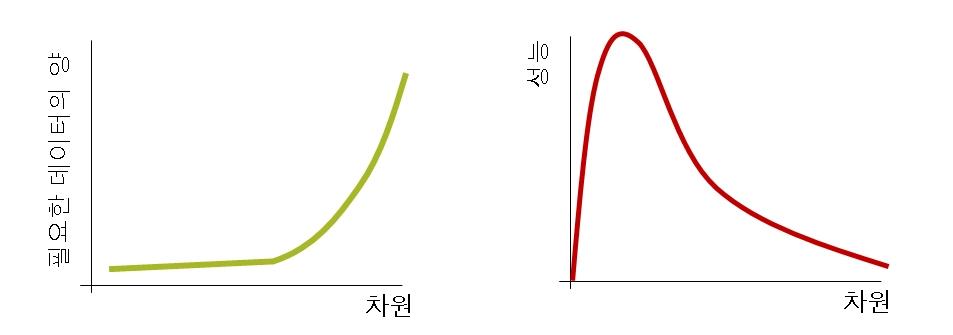
차원의 저주(Curse of Dimensionality)
•
기존 있는 데이터의 양을 포함하는 차원이 증가 할수록, 데이터의 부족으로 인해 Overfitting등의 문제로 모델의 성능이 떨어지는 현상(데이터의 품귀 현상)
•
차원이 증가할 수록 나타나는 특징
기하급수 | 선형 비례가 아닌 N제곱 기준으로 비례하여 증가함 |
희소(Sparse) 구조 | 동일 개수의 데이터 밀도는 차원 증가에 따라 희박해짐 |
고차원 | 수십 개 정도의 저차원에서는 발생하지 않음 |
높은 상관관계 | 피처가 많을 경우 개별 피처 간에 상관관계가 높을 가능성이 큼 |
낮은 신뢰도 | 수백 개의 피처로 학습한 경우 상대적으로 낮은 성능이 나타남 |
차원 축소의 방법
•
피처선택(Feature Selection)
◦
특정 피처에 종속성이 강한 불필요한 피처는 제거하고, 데이터의 특징을 잘 나타내는 주요 피처만 선택
◦
기존 피처를 저차원의 중요 피처로 압축해서 추출 à 기존의 피처가 압축된 것이므로 다른 값으로 나타남
•
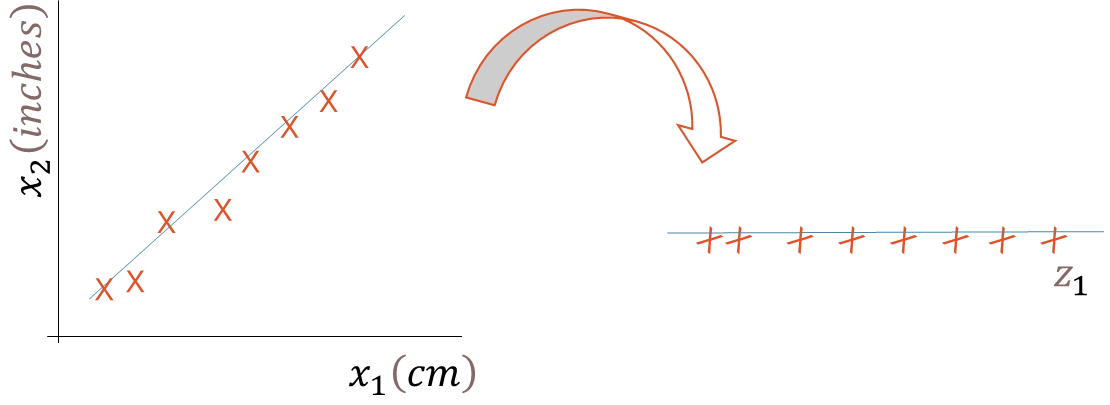
피처추출(Feature Extraction)
◦
피처를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑해서 추출
◦
기존 피처가 인지하기 어려웠던 잠재적인 요소(Latent Factor)를 추출
차원 축소의 목표
모든 속성을 사용하여 얻은 데이터 분석 결과 ≈ 차원 축소한 속성을 사용하여 얻은 데이터 분석 결과
차원 축소의 사례
•
이미지 데이터 분석 : 매우 많은 픽셀로 이뤄진 이미지 데이터 분석 시 차원 축소하는 것이 예측 성능을 높임
◦
PCA, LDA
•
텍스트 의미 추출 : 문서 내 단어들의 구성에서 숨겨진 의미나 토픽의 잠재요소를 간주하고 찾음
◦
SVD, NMF
PCA(Principal Component Analysis) 정의
•
상관관계가 있는 고차원 자료를 자료의 변동을 최대한 보존하는 고유값과 고유벡터를 이용하여 저차원 자료로 변환시키는 분석 기법(차원의 축소)
PCA
•
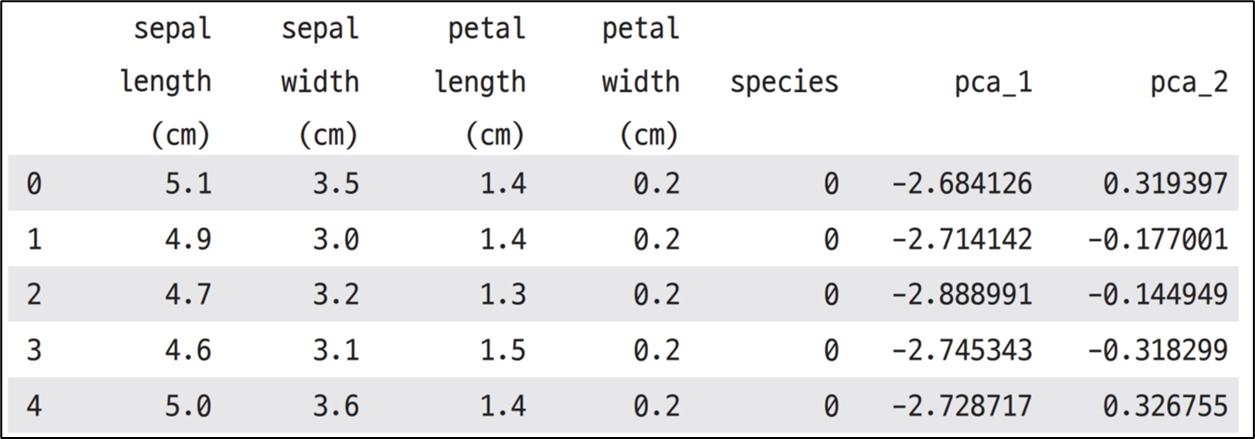
PCA 예시 1
PCA 변환 사례
•
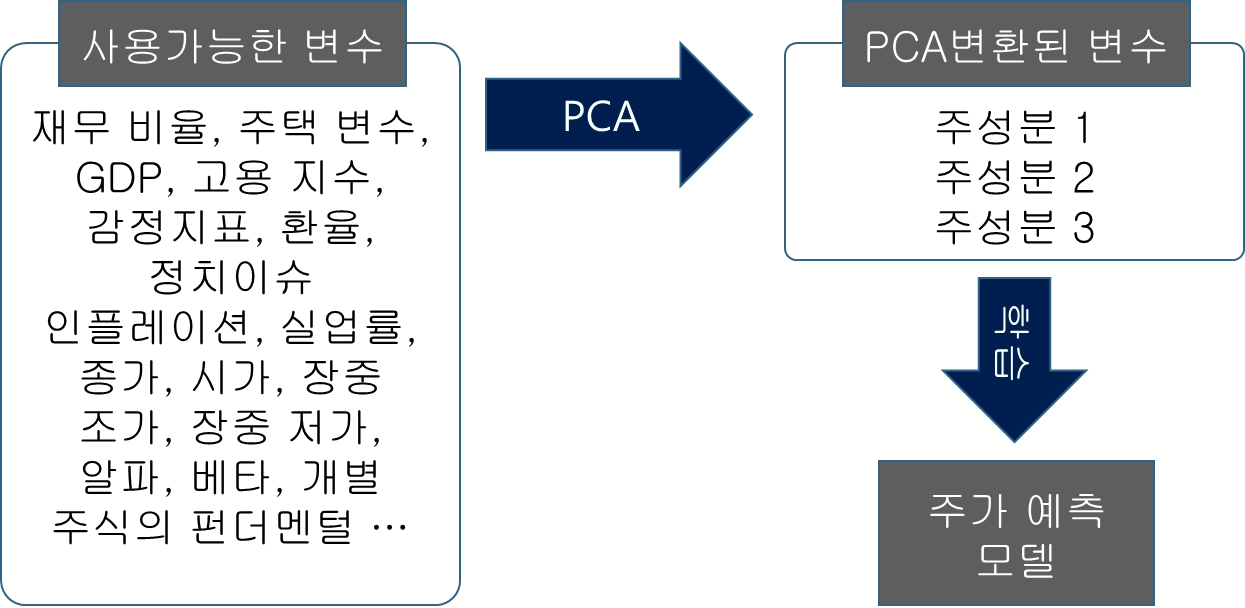
PCA 예시 2
주가 예측 모델
•
•
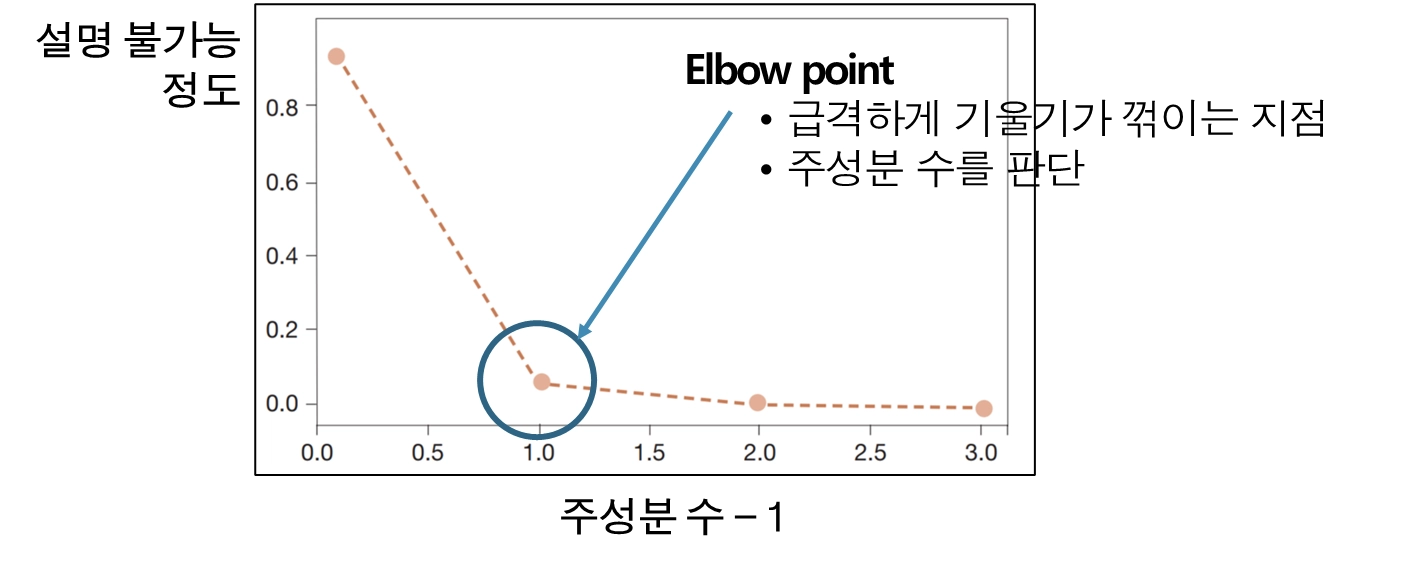
Scree plot
◦
PCA로 차원을 변환시킨 결과값을 바탕으로 각 컴포넌트의 수가 얼마만큼 원본 데이터의 정보를 설명할 수 없는지 나타냄
PCA(Principal Component Analysis) 방법
공분산 계산 → 고유벡터 계산 → 고유치 선택 → 변환행렬 생성 → 선형 변환
•
x와 y의 공분산은 x, y의 흩어진 정도가 얼마나 서로 상관관계를 가지고 흩어졌는지를 나타냄
수행 절차 | 절차 별 수행 Logic |
① 공분산 계산 | x, y의 공분산은 x, y의 흩어진 정도가 얼마나 서로 상관관계를 가지고 흩어졌는지를 나타냄 |
② 고유벡터(eigen vector) 계산 | 행렬 A를 선형변환한 결과가 자기 자신의 상수배가 되게 하는 벡터 |
③ 고유값(eigen value) 선택 | 행렬 A를 선형변환한 결과가 자기자신의 상수배가 되게 하는 값 |
④ 변환행렬
(transform matrix) 생성 | 고유벡터를 변환행렬로 사용 |
⑤ 선형변환 | 선형변환에 의해 특징벡터 추출 |
공분산(Covariance)
고유값과 고유 벡터
PCA 적용 시 주의 사항
•
원본 데이터가 주성분으로 변환되므로 원본 데이터에 대한 해석이 어려움
◦
변환된 주성분으로 원본 데이터가 가지고 있는 정보를 표현하고 해석하기 어려움
•
정보 손실
◦
주성분은 데이터 셋 피처 간의 최대 편차를 포함하기는 하지만, 주성분의 수를 잘못 선택한 경우, 원본 피처와 비교하여 정보가 누락될 수 있음
•
PCA 변환 전에 모든 범주형 변수를 수치형 변수로 변환하고, 표준화를 수행해야함
◦
PCA 변환의 가정: 평균과 분산이 변수의 전체 분포를 설명한다 → 데이터의 정규분포
◦
PCA는 스케일에 영향을 받으므로 z-score 변환을 수행하여 평균 0, 표준편차 1 형태로 스케일을 맞춰줌