Search
🤫

중복데이터 처리

중복값(Duplicated Instances)

•
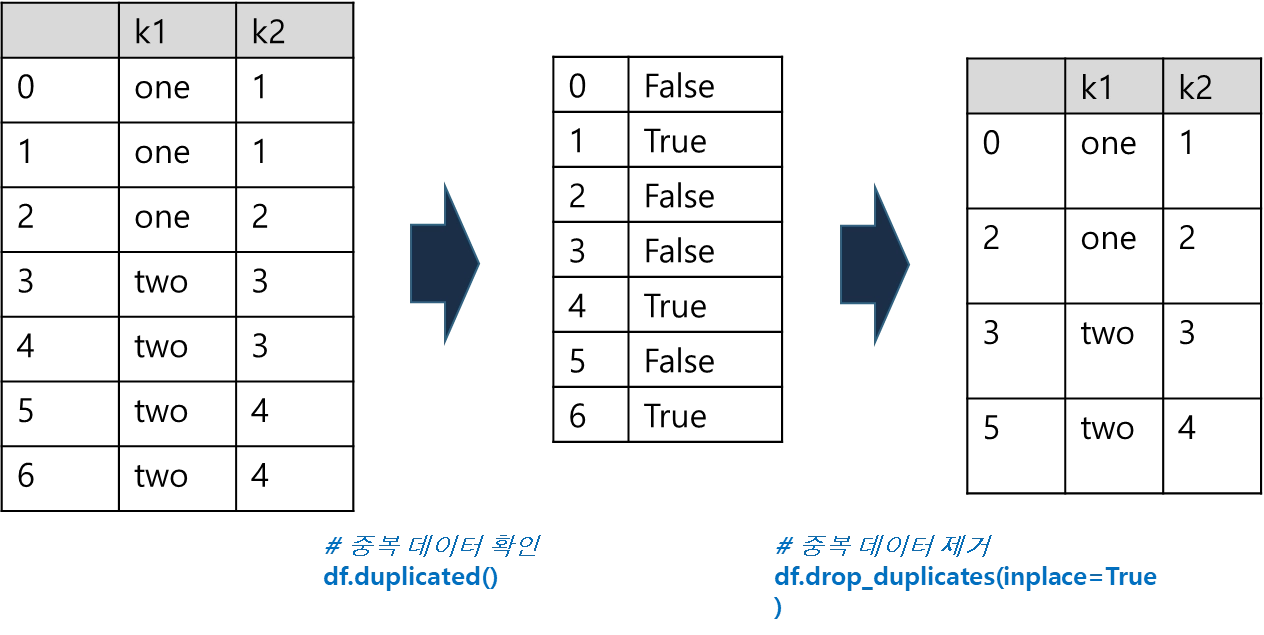
하나의 테이블에 동일한 값이 들어있는 경우, 중복값으로 판단하고 데이터 전처리 과정에서 중복값을 제거하여 사용 하는 것이 일반적임
dup = DataFrame({'k1': ['one'] * 3 + ['two'] * 4, 'k2': [1, 1, 2, 3, 3, 4, 4]}) # 중복 데이터 확인 dup.duplicated() # 중복 데이터 제거 dup.drop_duplicates(inplace=True)
Python
복사

중복 속성(Redundant attributes)

•
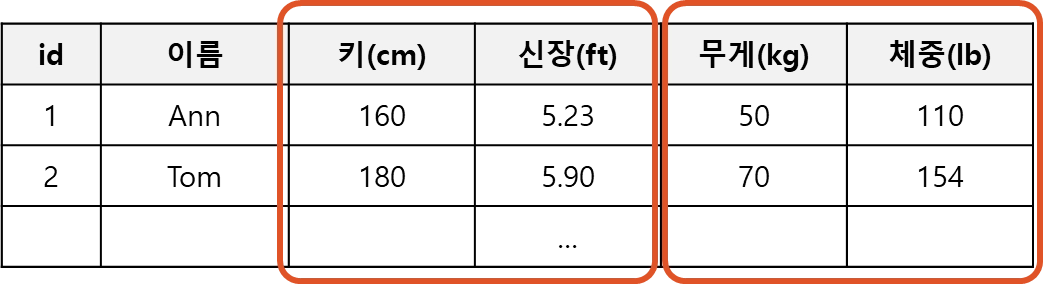
한 데이터의 특성(feature)을 다른 특성(feature) 에서 파생된 값으로 설정 할 수 있는 경우
•
발생 원인
◦
여러 데이터 저장소를 사용하는 데이터 통합 시 발생
◦
특성(feature)명 지정방법이 모호하거나 또는 다른 명칭으로 저장하여 불일치가 발생하여 데이터 세트가 중복

중복 속성 감지 방법

변수의 관련성

상관(Correlation)
•
두 변수 사이의 관계를 상정하는 것
•
‘한 쪽이 증가하면 다른 쪽은 감소한다’, 또는 ‘한 쪽이 증가하면 다른 쪽은 증가한다’
상관분석(Correlation Analysis)
•
두 변수 간에 어떤 선형적 관계를 갖고 있는지를 공분산 또는 변수의 순위 등의 계수를 이용하여 분석하는 분석 기법
•
한 속성이 다른 속성을 얼마나 강하게 의미하는지 측정
산점도
•
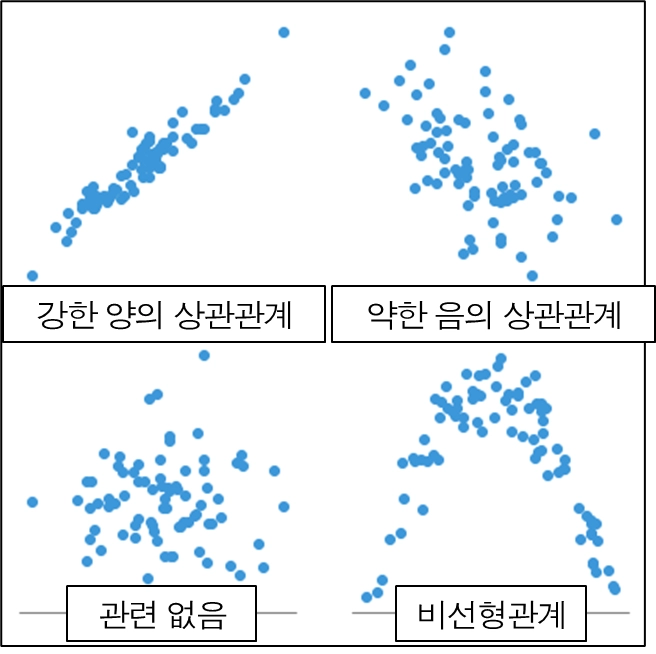
속성 간의 상관 관계를 이해하는 데 유용한 도구
상관계수(Correlation coefficient)
•
두 변수 간의 관련성이 얼마나 강한지 나타내는 지표
◦
공분산을 최대값 1, 최소값 -1 사이가 되도록 표준화
◦
양의 상관관계 : A가 증가함에 따라 B가 증가함(상관계수 > 1)
◦
음의 상관관계 : A가 증가함에 따라 B가 감소함(상관계수 < 1)
◦
상관관계 없음 : A와 B가 서로 독립적인 관계임(상관계수 = 0)

상관분석 방법

•
수치형 데이터 : 피어슨(Pearson) 상관계수를 계산하여 평가
•
범주형 데이터 : 카이제곱검정을 계산하여 평가

피어슨 상관계수(Pearson correlation coefficient)

•
공분산을 이용하여 두 변수의 상관관계를 -1과 1 사이의 값을 갖도록 하는 상관계수
•
비선형 상관관계는 나타내지 못함
피어슨 상관계수(Pearson correlation coefficient)
ρ(X,Y)=Cov(X,Y)σX∗σYρ(X,Y) = \frac{Cov(X,Y)}{σ_{X} * σ_{Y}}
•
Cov(X,Y)Cov(X,Y)는 XX와 YY의 공분산
•
σXσ_{X}와 σY σ_{Y}는 각각 XX와 YY의 표준편차
공분산(Covariance)
•
두 확률변수 𝑥,  𝑦의 방향의 조합(선형성)
•
공분산 > 0 : 변수 𝑥 가 평균보다 큰 값일 때, 변수 𝑦 도 평균보다 큰 값을 갖음
•
공분산 < 0 : 변수 𝑥 가 평균보다 작은 값일 때, 변수 𝑦 도 평균보다 작은 값을 갖음
•
공분산의 부호만으로 두 변수 간의 방향성을 확인할 수 있음
•
x,yx, y가 서로 독립이면 𝐶𝑜𝑣(𝑥,𝑦)= 0 임
Cov(X,Y)=∑i=1N(xi−μx)(yi−μy)NCov(X,Y) = \frac{\sum_{i=1}^{N}(x_i - μ_x)(y_i - μ_y)}{N}
•
xix_i와 yiy_i는 각각 X와 Y의 i번째 값
•
μxμ_x와 μyμ_y는 각각 X와 Y의 평균
•
NN은 데이터 포인트의 총 개수
•
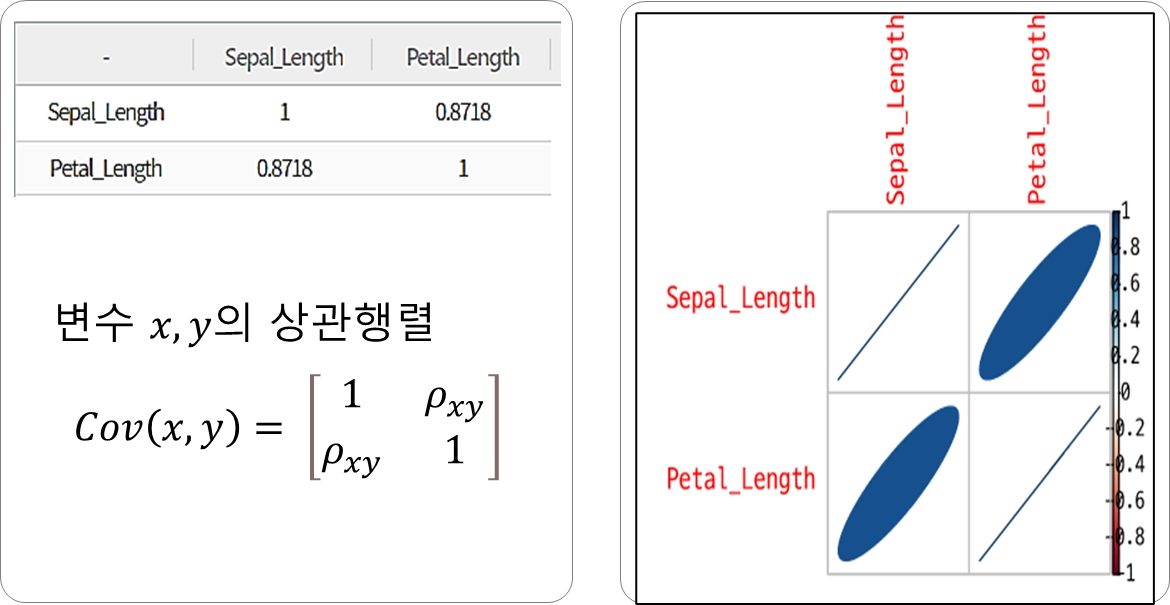
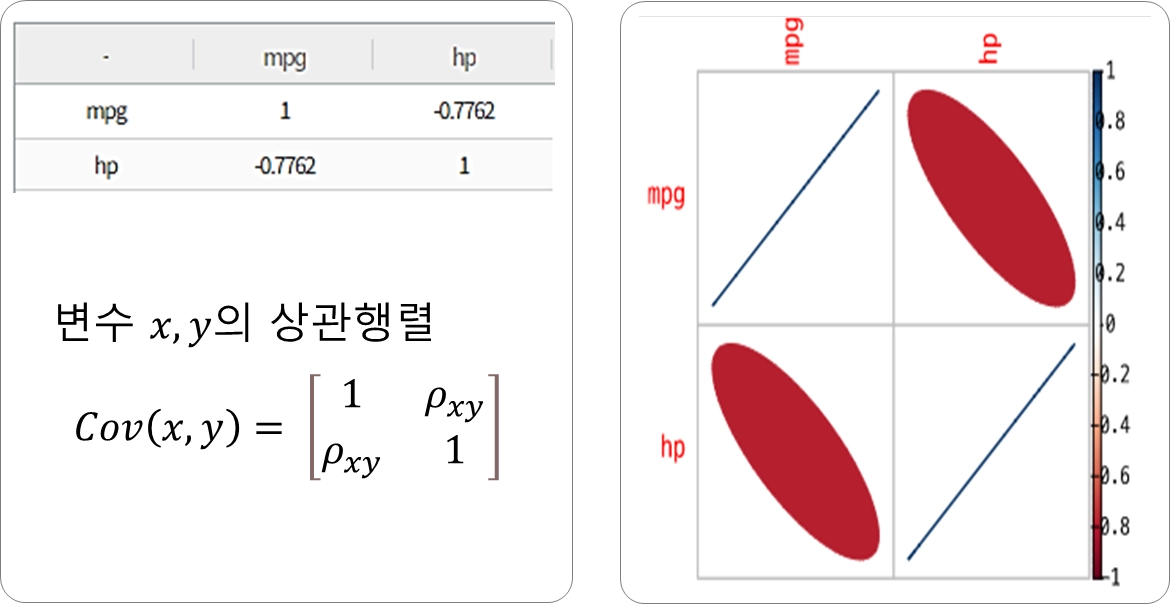
사례: Iris 데이터 셋
Sepal_Length와 Petal_Length는 강한 양의 상관관계
mpg와 hp는 강한 양의 상관관계
상관분석의 검정 통계량

카이제곱(χ2χ2) 검정

범주형 데이터의 상관관계를 분석
카이제곱 검정
χ2=∑(관측값−기대값)2기대값χ^2 = ∑ \frac{(관측값 - 기대값)^2}{기대값}
•
관측값: 실제로 관측된 값
•
기대값: 이론적으로 기대되는 값
예시
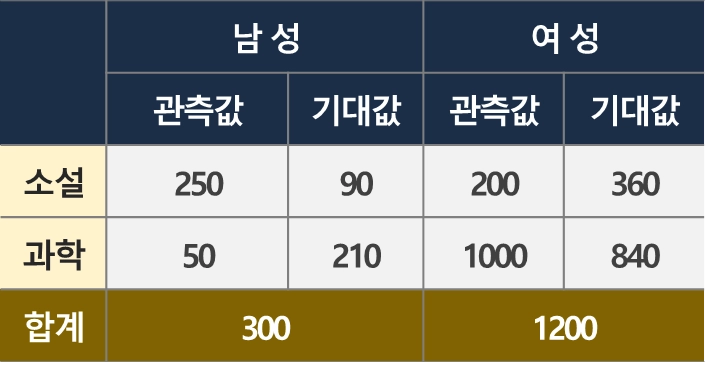
사례 : 성별과 선호하는 독서 분야의 상관관계
•
하나 이상의 범주에서 관측된 빈도가 기대 빈도와 일치하는지 확인
χ2=(250−90)290+(50−210)2210+(200−360)2360+(1000−840)2840=507.93χ^2= \frac{(250 -90)^2}{90}+ \frac{ (50-210)^2}{210}+\frac{(200 -360)^2}{360}+\frac{(1000 -840)^2}{840} = 507.93
[가설] 성별과 선호하는 독서분야는 독립적(상관관계가 없음)
•
χ2χ^2= 507.93
•
자유도(df) = (2 − 1) (2 − 1) = 1
•
0.5 % 유의 수준에서 가설을 기각하는데 필요한 값 : 7.88
[결론]
•
성별과 선호하는 독서분야가 독립적이라는 가설은 기각
•
성별과 선호하는 독서분야는 강한 상관관계가 있음