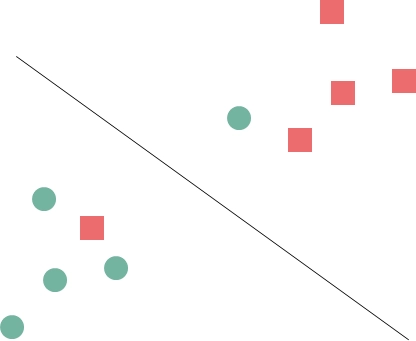
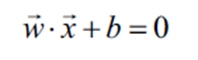생각해보기
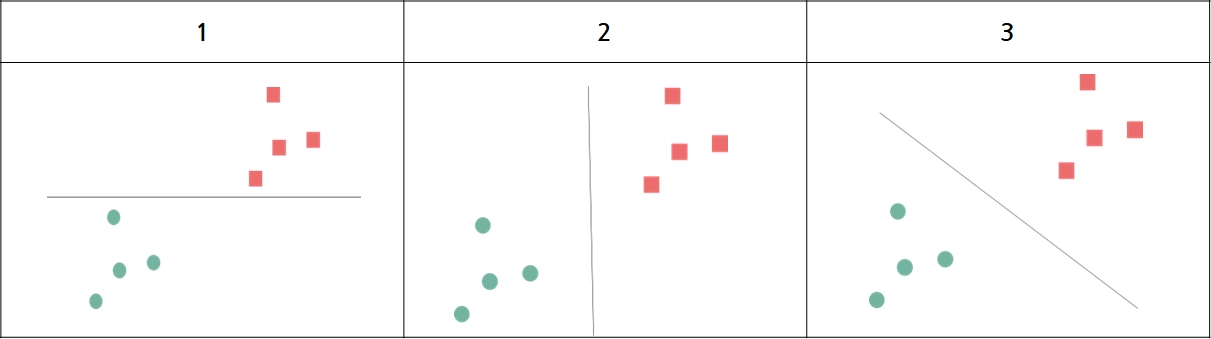
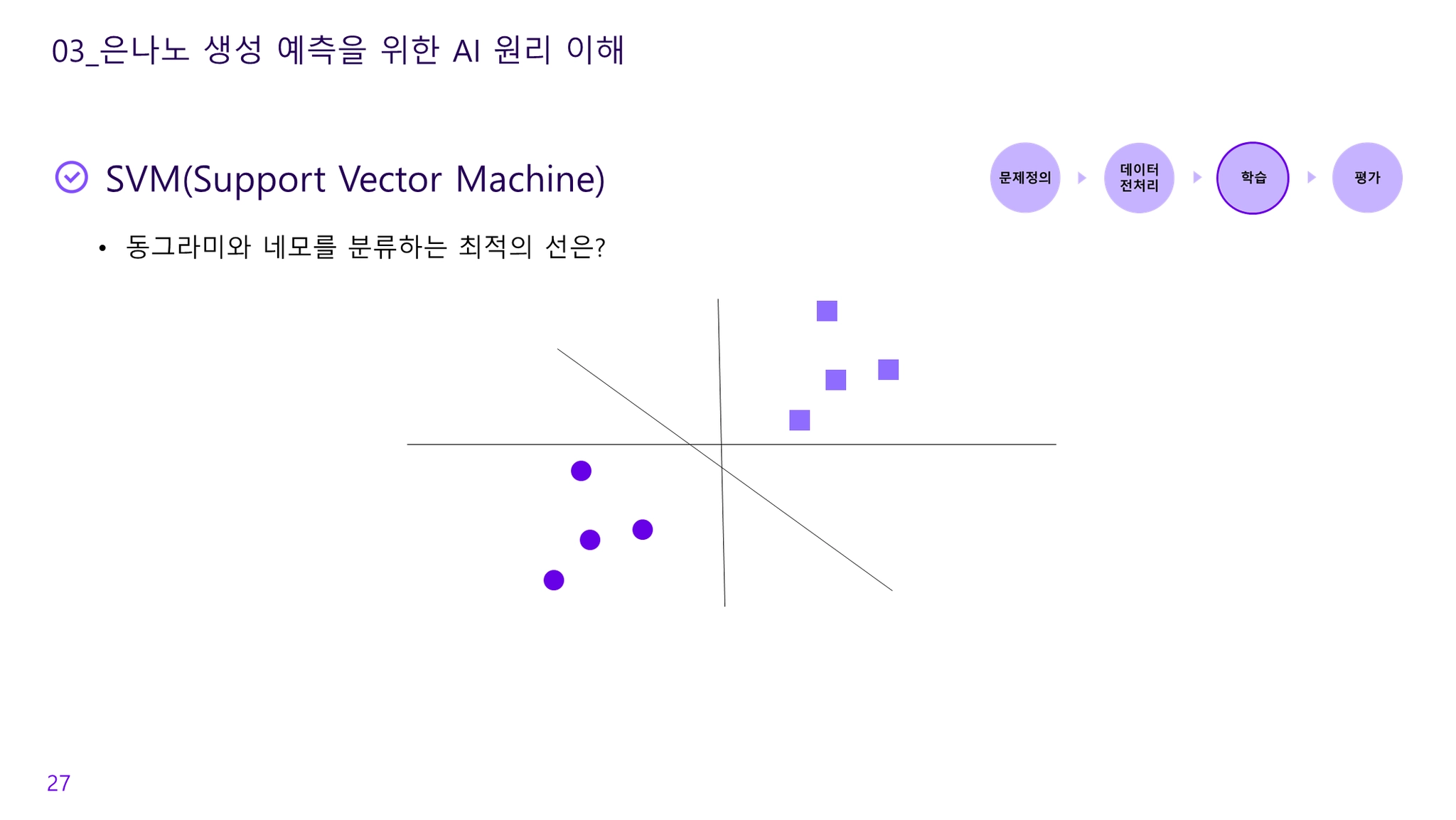
Q. 동그라미와 네모를 구분하는 최적의 선은 무엇인가?
→ 1, 2, 3번 모두 동그라미와 네모를 분류할 수 있는 선이다. SVM은 두 그룹으로 분류할 수 있는 경계선을 기준으로 경계선과 가장 가까운 데이터들을 가장 큰 마진(margin)으로 설정할 수 있는 경계선을 최적의 선으로 정의한다.
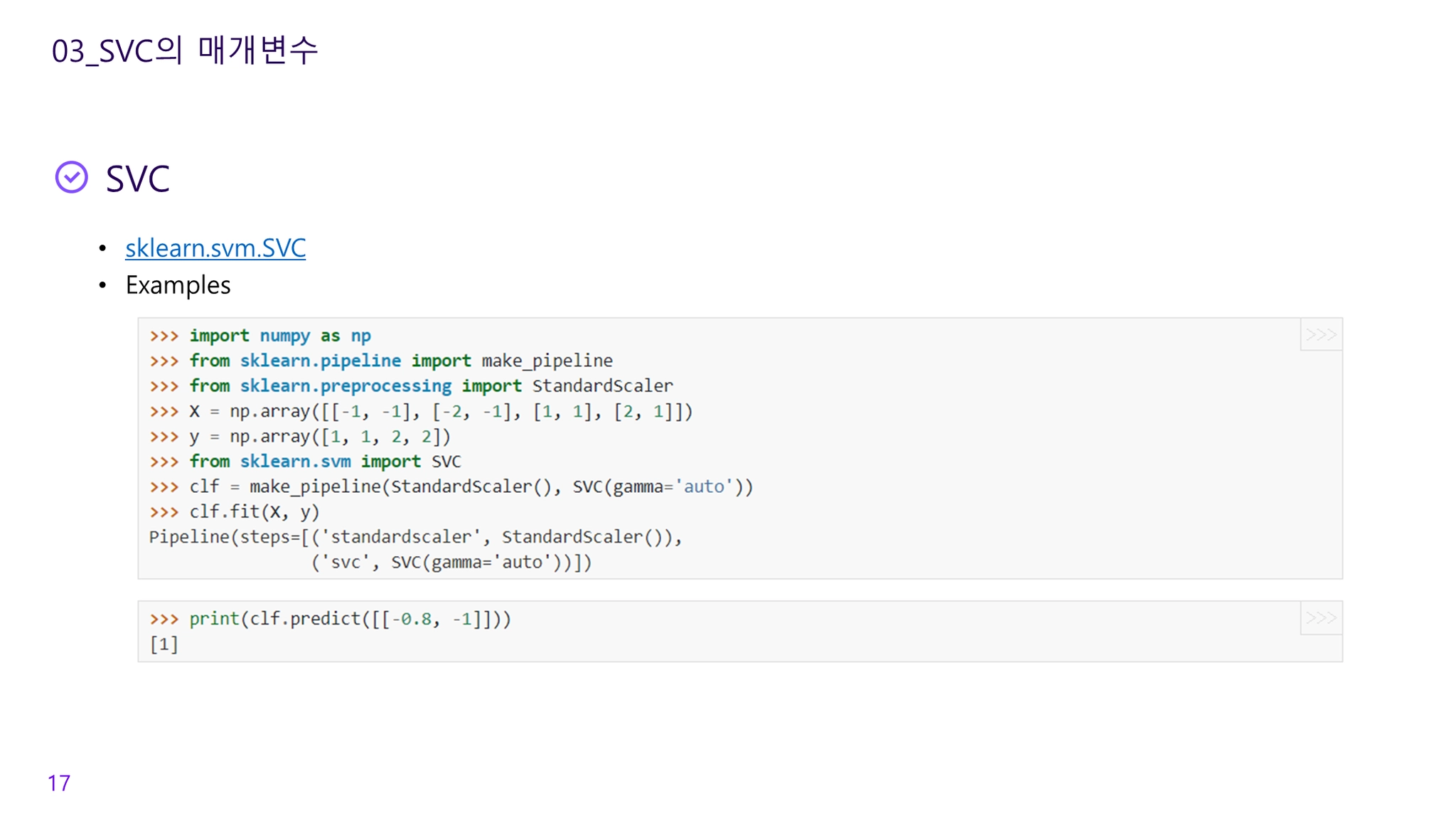
Support Vector Machine
•
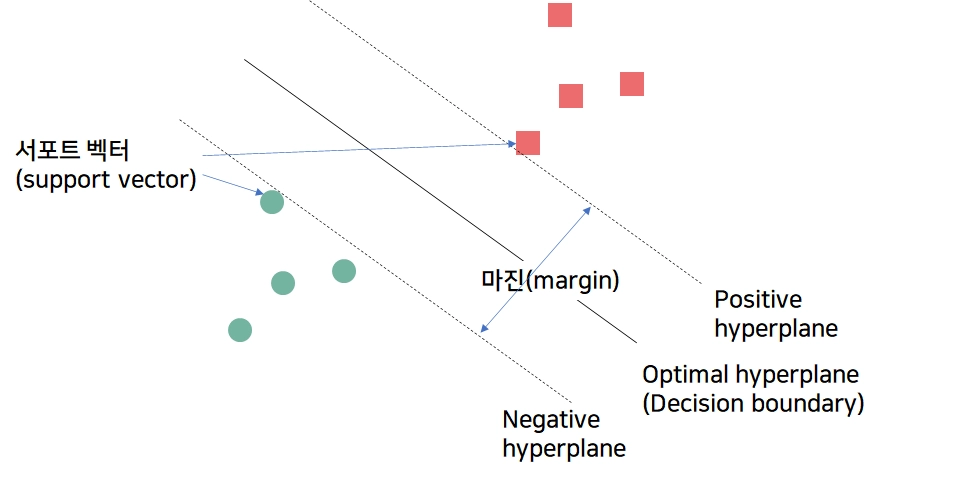
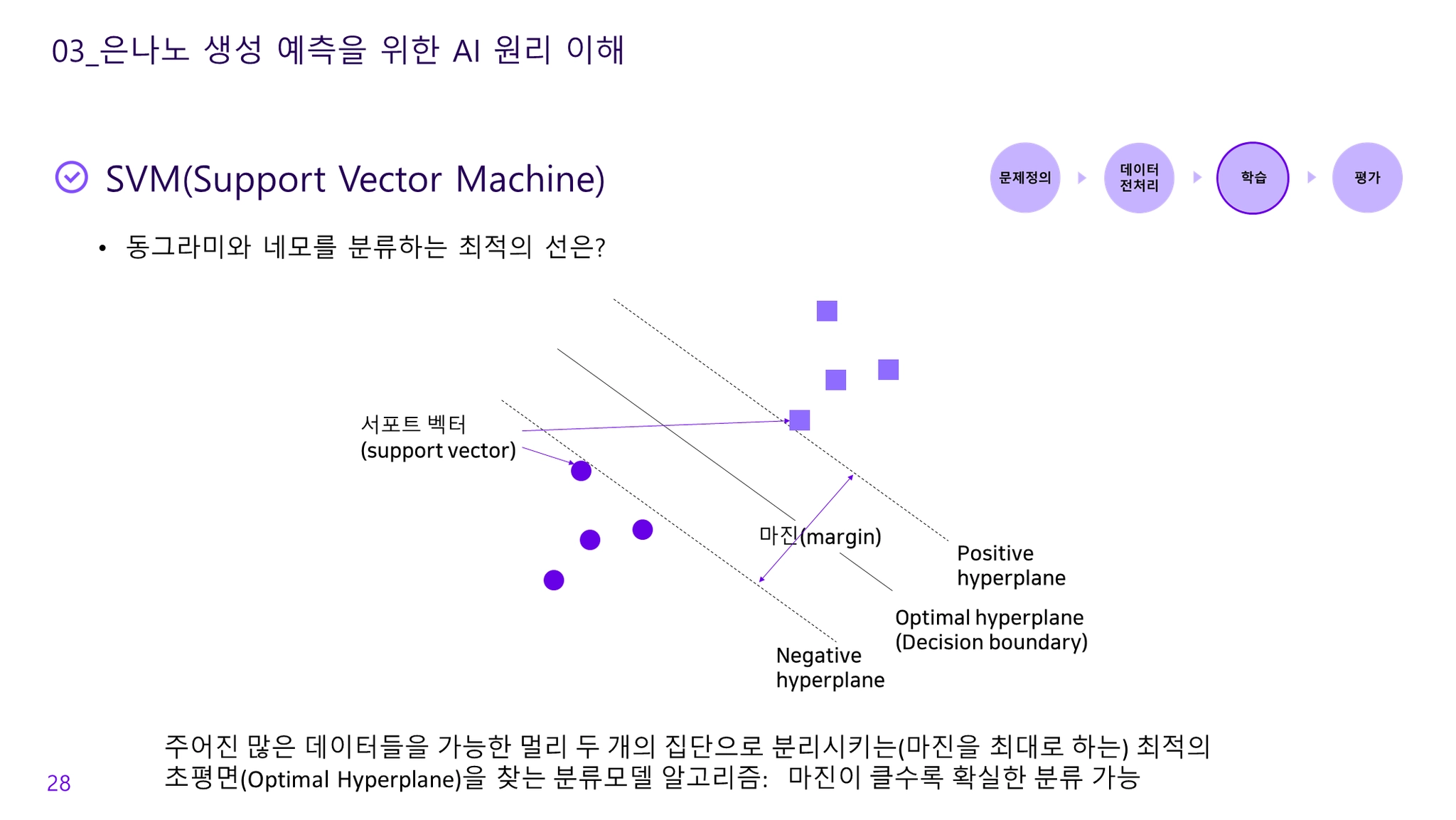
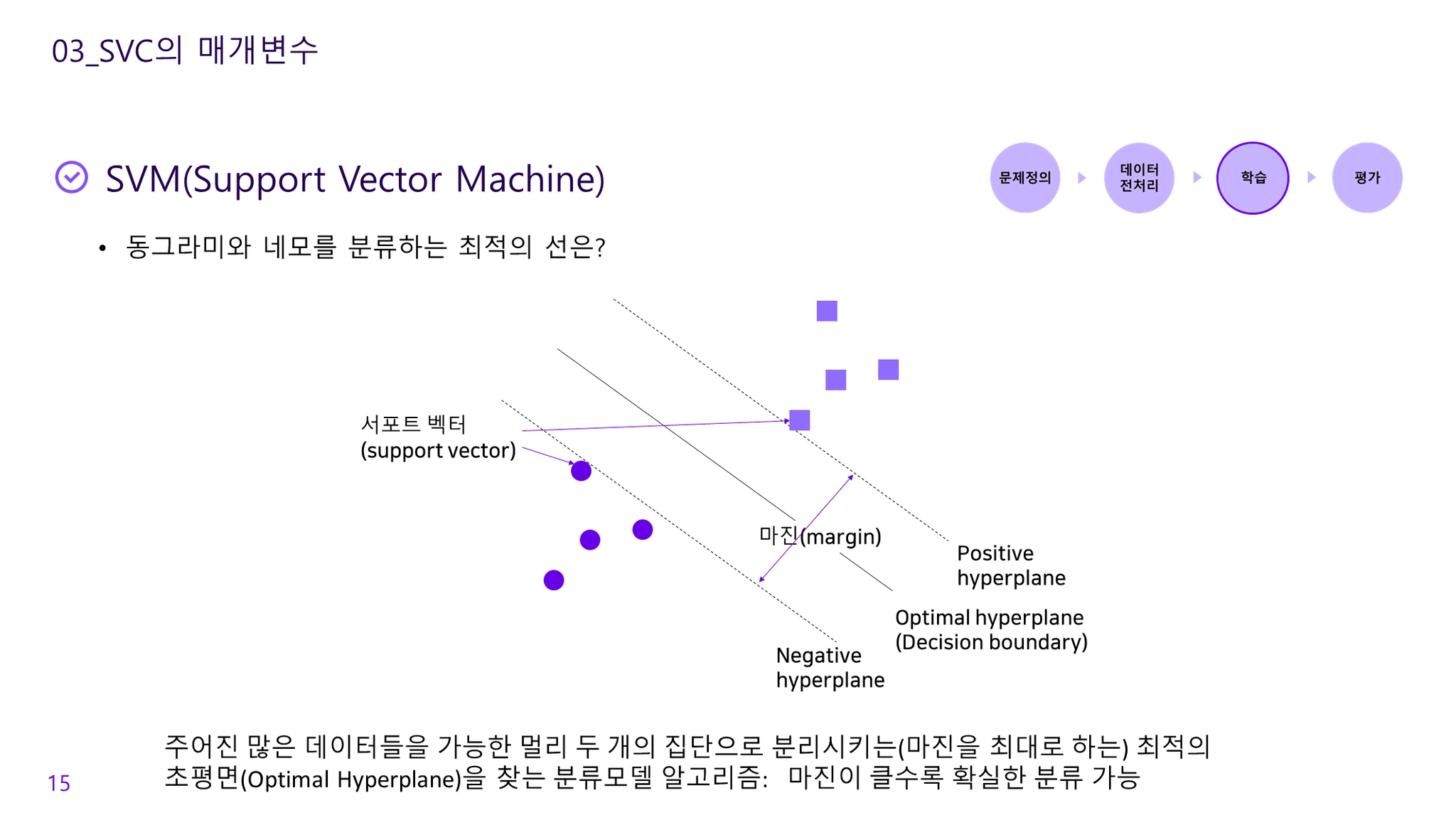
주어진 많은 데이터들을 가능한 멀리 두 개의 집단으로 분리시키는(마진을 최대로 하는) 최적의 초평면(Optimal Hyperplane)을 찾는 분류모델 알고리즘
•
주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만드는 분류 모델 알고리즘
마진(margin)의 최대화!
장점
•
서포트 벡터 간의 간격을 최대화하여 분류하기 때문에 특이한 데이터에 대해서도 잘 분류할 수 있음
◦
강아지와 고양이를 구분하는 문제에서 개냥이, 냥아지와 같이 구분하기 어려운 속성의 데이터도 간격을 최대화하여 분류를 하기 때문에 분류 정확도가 높은편
•
노이즈에 크게 영향을 받지 않는 편이고, 과적합 문제가 적음
•
일반적으로 데이터의 속성의 수와 샘플 수가 많지 않은 경우에 우수한 성능을 보임
단점
•
처리할 데이터 양(속성, 샘플)이 늘어나거나 비정형 데이터인 경우는 복잡도가 높아져 활용하기가 쉽지 않음(이 경우 인공신경망이 더 효과적)
•
최적의 알고리즘을 찾기 위해 커널함수 및 매개변수에 대해 다양한 조합의 테스트가 필요함
•
해석이 불가능하지 않지만, 알고리즘 결과 해석이 어렵고 학습에 시간이 많이 소요됨
SVM 구성요소
Optimal Hyperplane(초평면)
•
속성 값에 따라 다차원 공간의 예제를 여러 가지 점 간의 경계를 정의하는 평면을 생성
•
데이터를 두 클래스 중 어느 곳에 속하는지 결정하기 위한 최적의 분류 기준선
•
n차원의 공간에서의 subspace 의미
•
초평면은 하나의 회귀식 (예: )
•
Positive hyperplane, Negative hyperplane
•
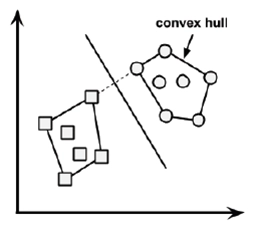
컨벡스 홀 사이의 가장 짧은 거리를 직각 이등분선으로 초평면 구함
•
2차원 공간에서는 기울기와 절편과 같은 직선 방정식이 초평면임
Margin(마진)
•
데이터를 두 클래스로 구분하는 최대 거리
•
positive hyperplane 과 negative hyperplane의 거리
•
소프트 마진 : 노이즈 등의 이유로 확실한 경계선과 마진을 둘 수 없는 경우
•
하드 마진 : 경계선을 기준으로 확실한 구분이 가능한 경우
Support vectors(서포트벡터)
•
집단을 구분하는 직선에서 가장 근거리에 위치하는 벡터
비선형 경계
방법1)
•
정확한 분류가 불가능한 경우, 허용된 범위내의 오차를 용인하며 총 비용 값을 최소화하도록 최적화를 시도
방법2)
•
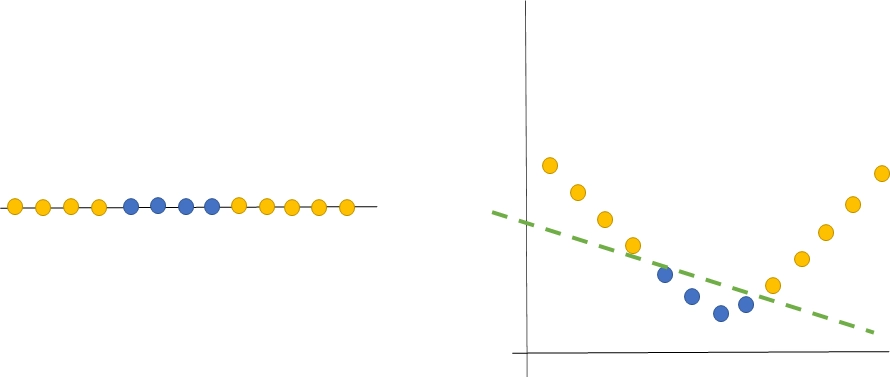
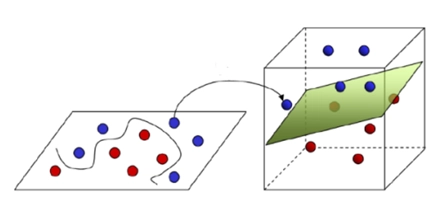
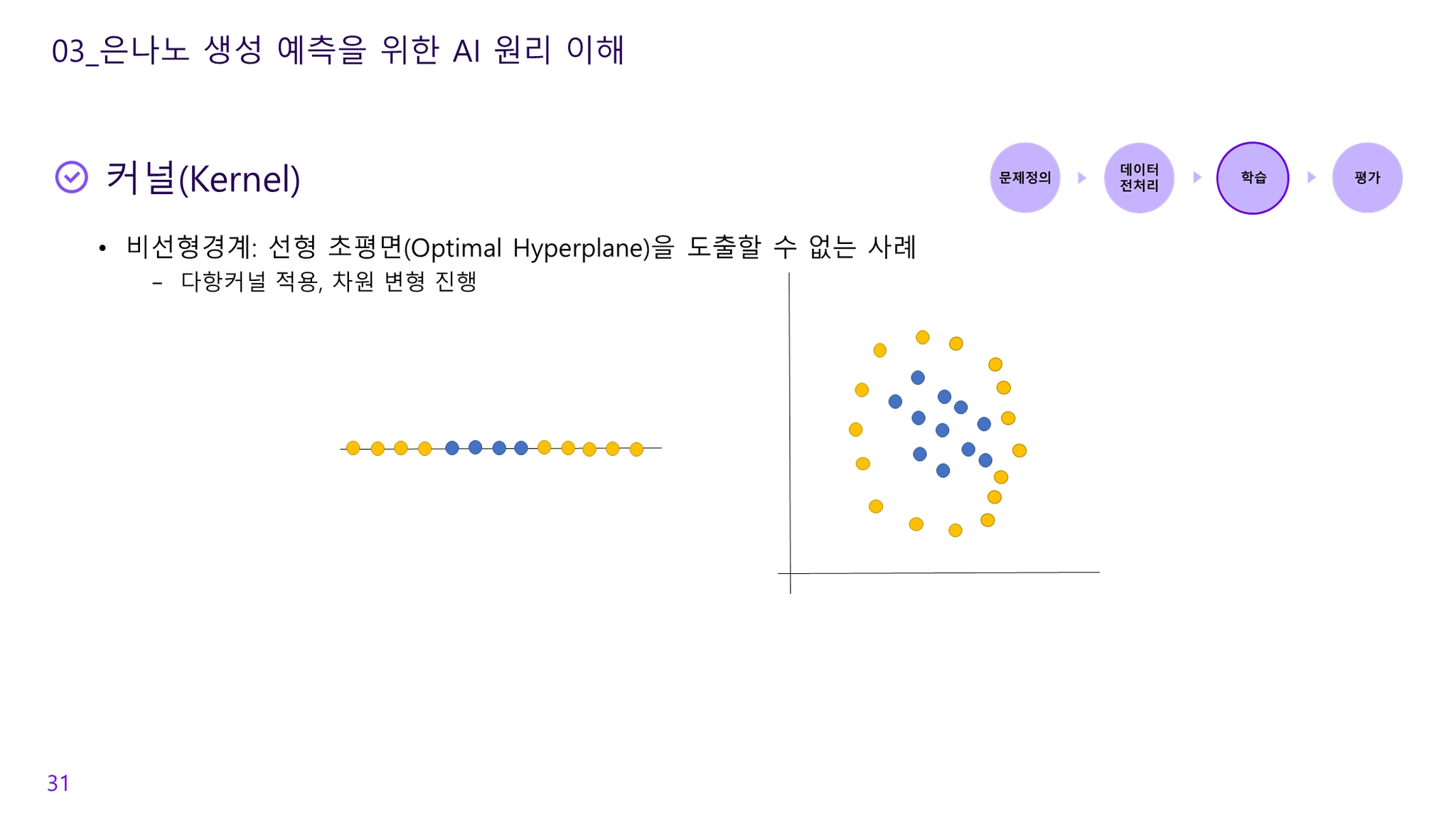
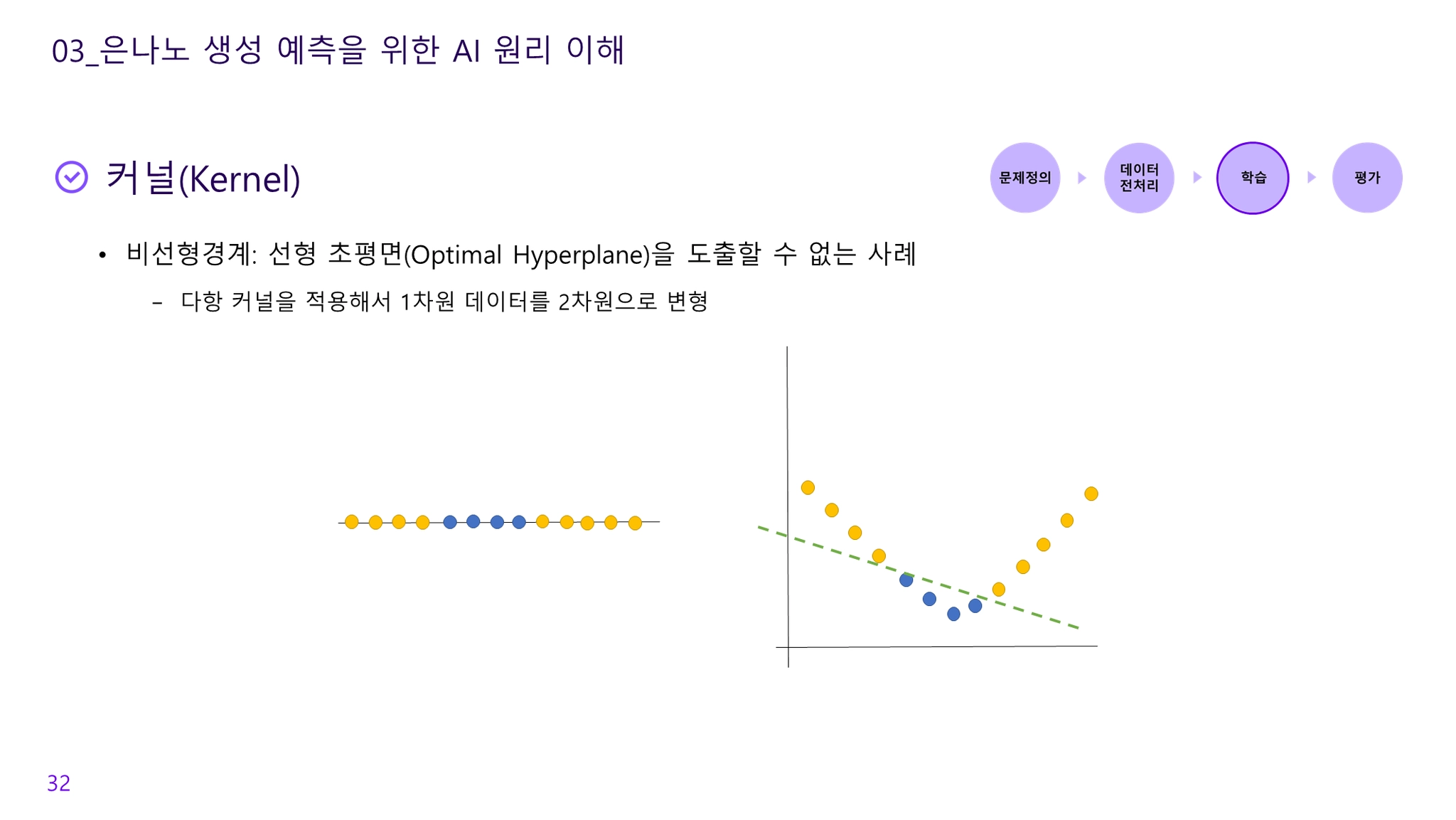
선형 초평면(Optimal Hyperplane)을 도출할 수 없는 사례의 경우 다항커널 적용하여 차원 변형 진행
◦
1차원을 2차원으로 변형
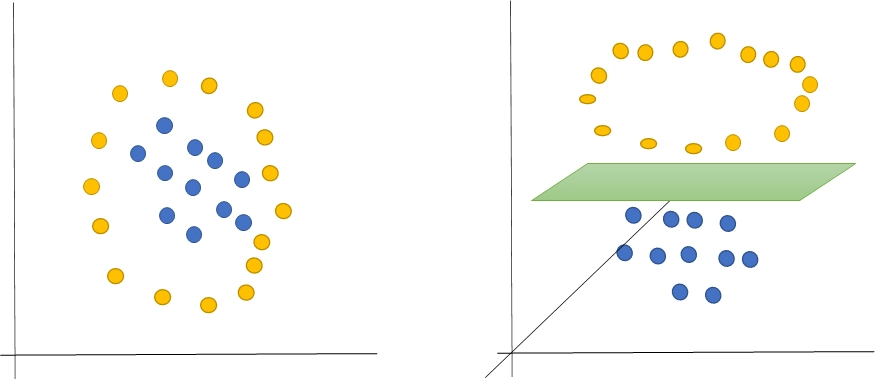
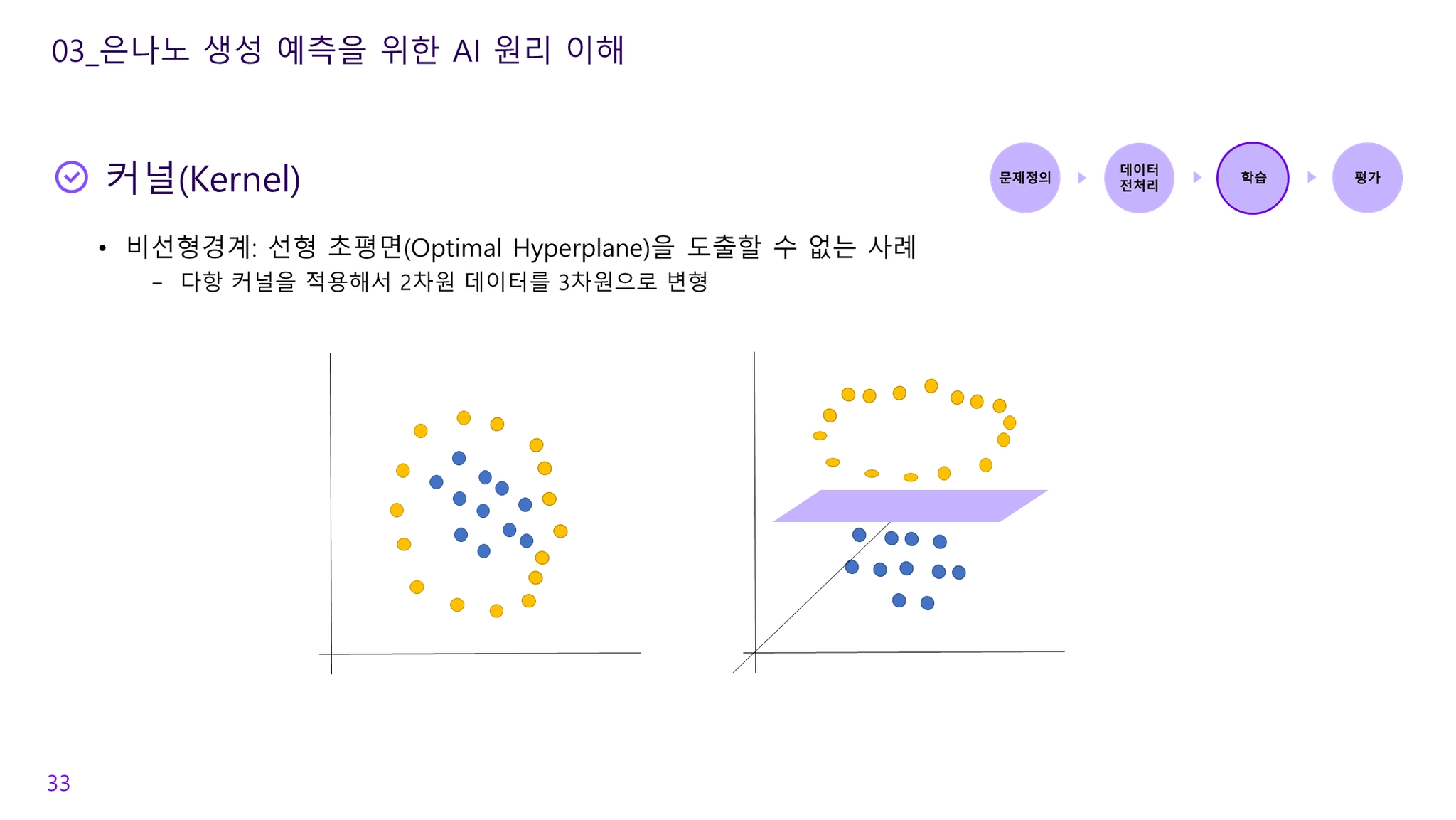
•
2차원을 3차원으로 변형
•
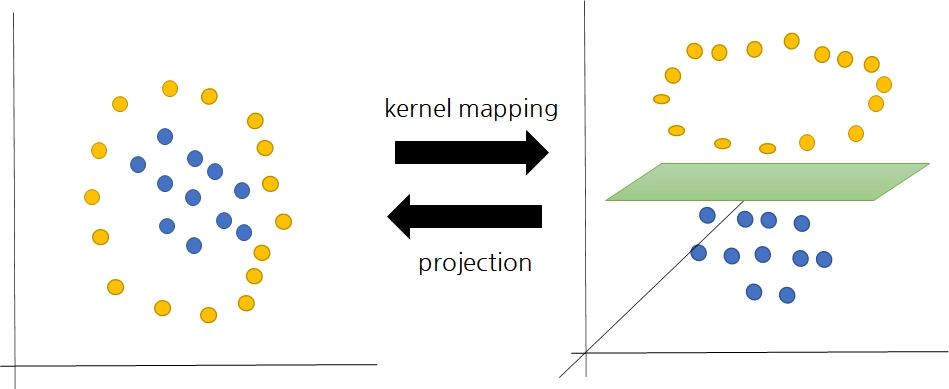
kernal mapping vs projection
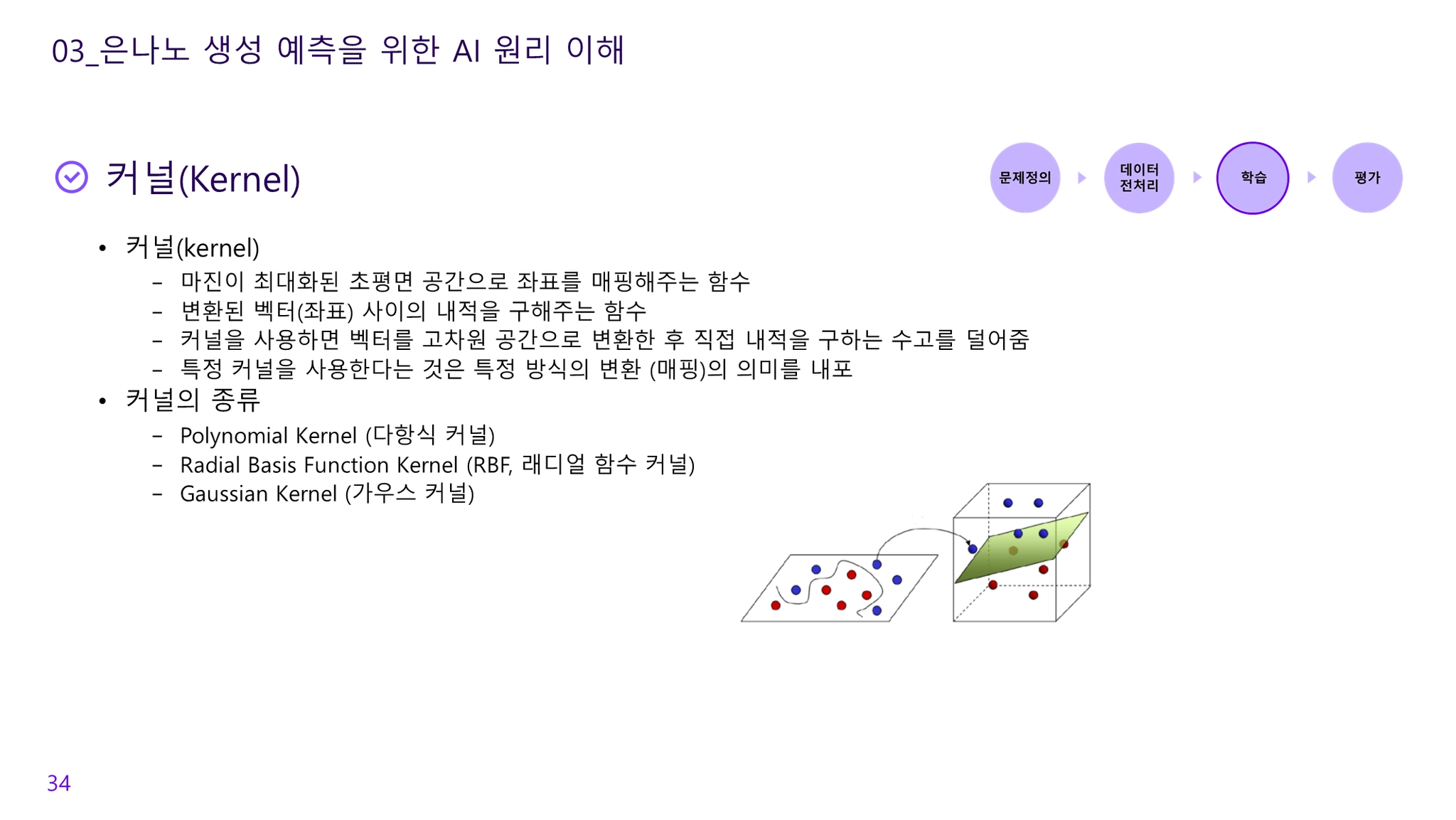
커널(kernel)
•
마진이 최대화된 초평면 공간으로 좌표를 매핑해주는 함수
•
변환된 벡터(좌표) 사이의 내적을 구해주는 함수
•
커널을 사용하면 벡터를 고차원 공간으로 변환한 후 직접 내적을 구하는 수고를 덜어줌
•
특정 커널을 사용한다는 것은 특정 방식의 변환 (매핑)의 의미를 내포
•
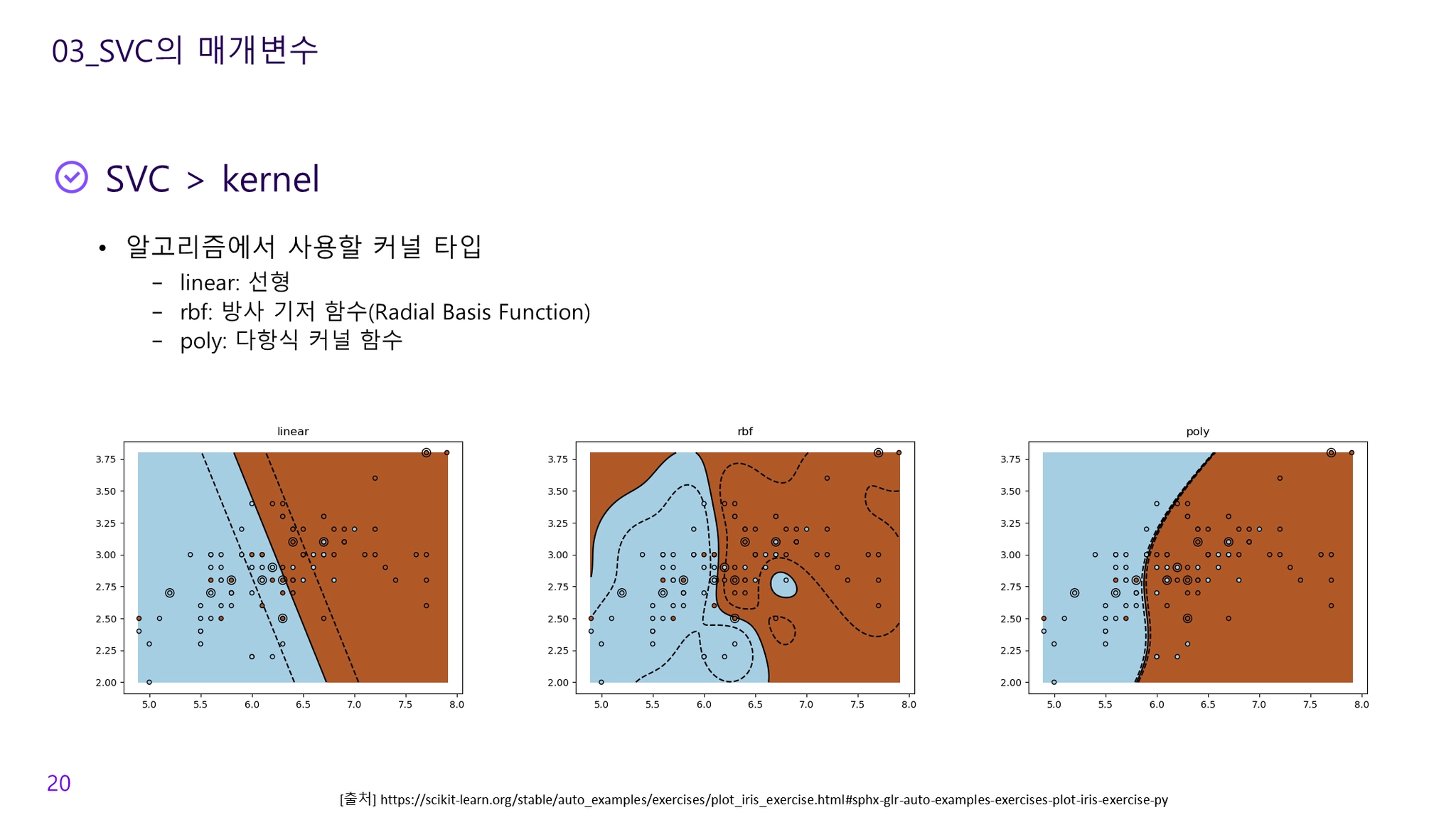
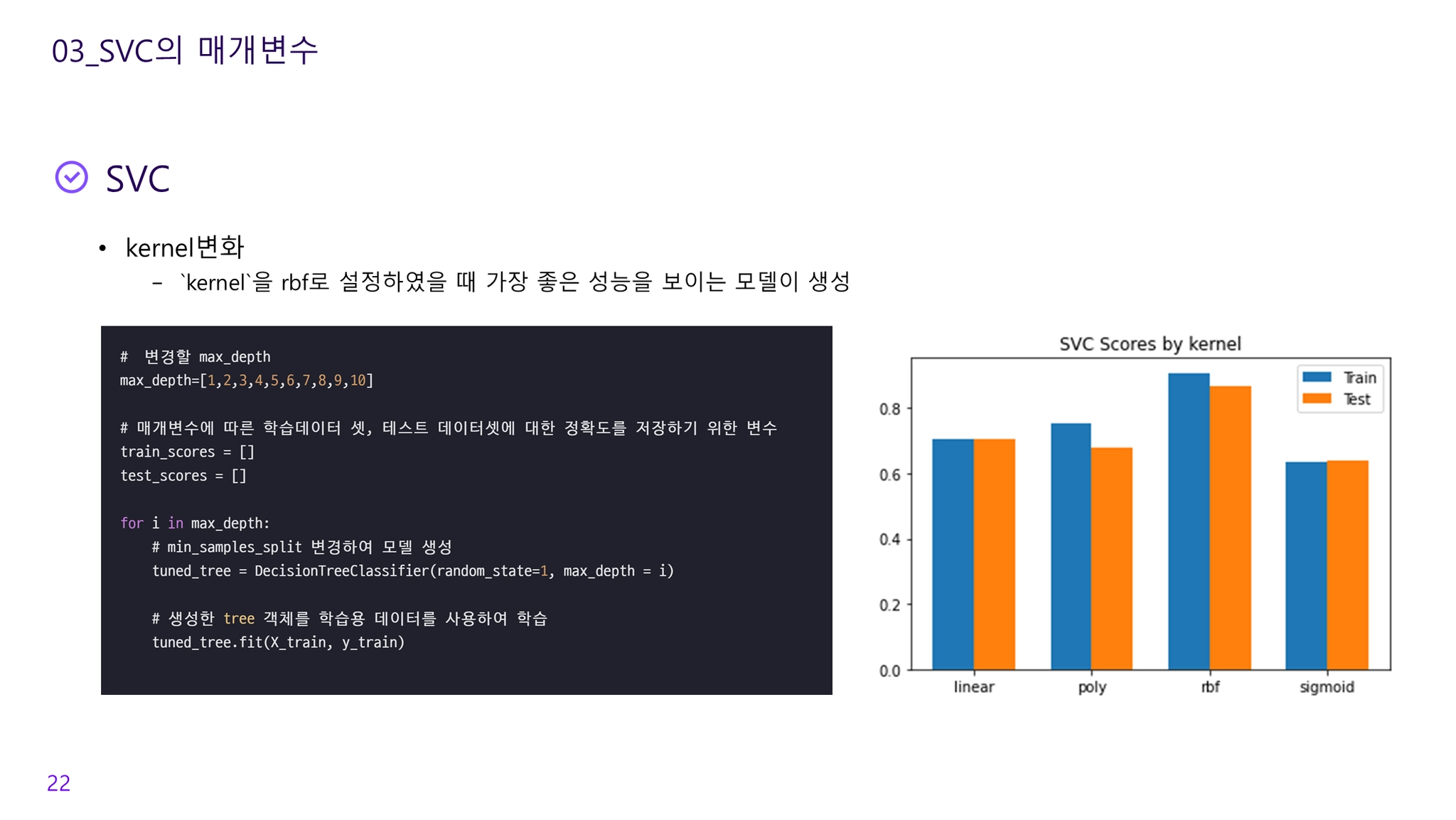
커널의 종류
◦
Polynomial Kernel (다항식 커널)
◦
Radial Basis Function Kernel (RBF, 래디얼 함수 커널): 감마 (γ) 파라미터 사용, 감마가 클수록 높은 편중과 작은 분산의 의미
◦
Gaussian Kernel (가우스 커널)