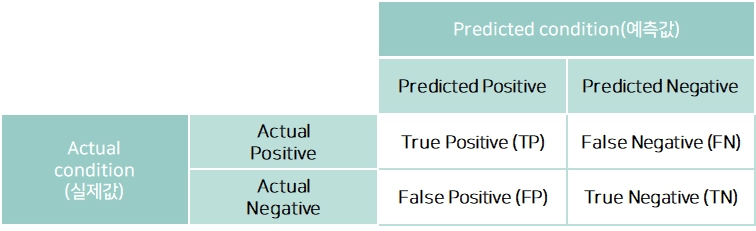
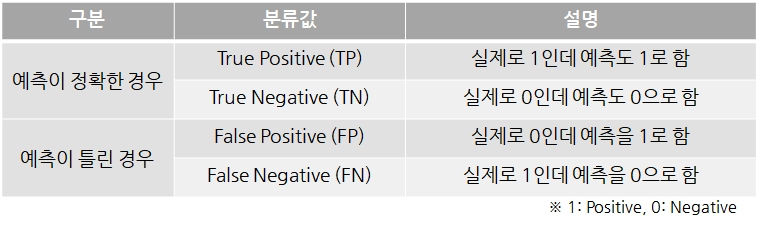
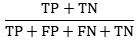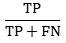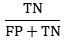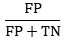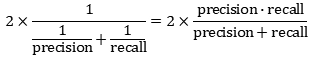혼동행렬(Confusion matrix)
•
데이터 분석에서 잘못된 예측의 영향을 간편하게 파악하기 위해 예측된 값과 실제 값이 일치하는지 여부를 행렬로 분류
•
학습된 분류 모델이 예측을 수행하면서 얼마나 헷갈리고 있는지도 함께 보여줌
•
혼동행렬을 작성함에 따라 모델의 성능을 평가할 수 있는 평가 메트릭이 도출됨
Accuracy(정확도)
•
전체 예측에서 (예측이 Positive이든 Negative이든 무관하게) 옳은 예측의 비율
•
분류 모델에서 기본 지표로 사용
•
sklearn.metrics.accuracy_score
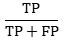
Precision(정밀도)
•
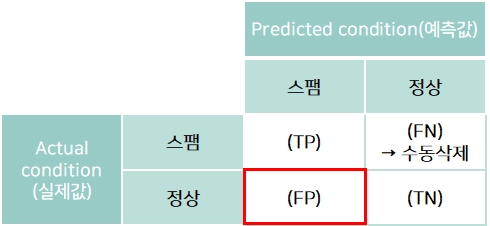
Positive로 예측된 것 중 실제로도 Positive인 경우의 비율(Positive Predictive Value)
•
실제 Negative 데이터를 Positive로 잘못 판단하게 되면 업무상 큰 영향을 주는 경우에 중요
◦
예: 스팸메일 필터링 모델(스팸: Positive, 정상: Negative)
Recall(재현율), Sensitivity (민감도)
•
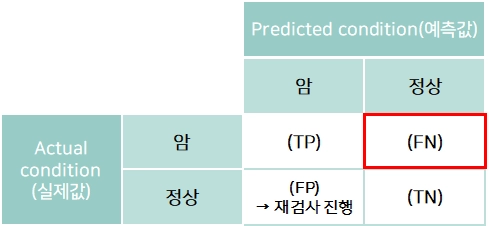
실제로 Positive인 것들 중 예측이 Positive로 된 경우의 비율(True Positive Rate)
•
실제 Positive 데이터를 Negative로 잘못 판단하게 되면 업무상 큰 영향을 주는 경우에 중요
◦
예: 암 판단 모델(암: Positive, 정상: Negative)
데이터 분포가 치우친 경우, 정밀도(Precision)와 재현율(Recall)을 활용하여 모델 평가
정밀도와 재현율은 상충 관계이므로, 문제의 성격에 따라 어느 쪽을 중시해야 하는지도 달라짐
Specificity(특이도)
•
실제로 Negative인 것들 중 예측이 Negative로 된 경우의 비율(True Negative Rate)
FP Rate
•
Positive가 아닌데 Positive로 예측된 비율(False Alarm Rate)
•
1−Specificity 와 같은 값
F1 score(F1 점수)
•
Precision과 Recall의 조화평균
•
Precision과 Recall의 상충관계를 반영하여 균형 잡힌 성능을 평가하여 실제 분류기를 비교하는데 사용
◦
정밀도와 재현율이 어느 한쪽으로 치우치지 않은 수치를 나타날 때 높은 값이 나타남
◦
정밀도 100%의 함정
▪
확실하게 Positive 라고 생각하는 경우를 Positive라고 예측하고, 나머지는 모두 Negative라고 예측
•
예) 확실하게 암일 것 같은 사람 1명한 Positive 라고 하고 나머지는 모두 Negative라고 함
•
정밀도= 𝑇𝑃/(𝑇𝑃+𝐹𝑃)= 1/(1+0) =1
◦
재현율 100%의 함정
▪
모든 경우를 Positive라고 예측
•
예) 전체 검사 인원 100명을 모두 Positive라고 예측(이중 실제로 Positive인원이 30명이라고 할 때)
•
재현율= 𝑇𝑃/(𝑇𝑃+𝐹𝑁)= 30/(30+0) =1
•
시스템의 성능을 하나의 수치로 표현하기 위해 사용하는 점수로 0~1사이의 값을 가짐
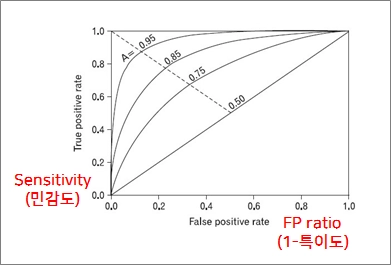
ROC(Receiver Operating Characteristic) 커브
•
X축에는 FP ratio(1-특이도), y축에는 민감도를 나타내 이 두 평가 값의 관계로 모형을 평가하는 기법
•
ROC Curve아래 면적(AUC)에 의해 측정
◦
AUC the Area Under a ROC Curve : ROC커브 이하의 면적
◦
0.5이면 성능이 전혀 없음. 1이면 최고의 성능
•
TPR과 FPR은 서로 반비례 관계에 있으므로, 여러가지 상황을 고려해서 성능 판단을 진행해야함
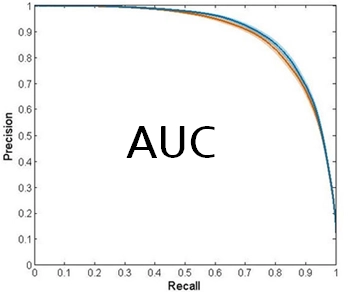
Precision Recall Plot(PR 그래프)
•
Recall(재현율, TP / (TP + FN))와 Precision(정밀도, TP / (TP + FP))를 이용하여 분류 모델의 수준을 면적으로 표현하여, 모델 평가를 가시화한 도구
•
데이터 분포가 심하게 불균등 할 때 사용
(예: 이상거래 검출 시나리오, 정상거래 비율이 비정상거래 비율보다 압도적으로 많음)