일반화(Generalization)
계층적인 개념을 반영하여 하위수준의 데이터를 상위수준으로 대체하는 방법
•
예) Street(하위수준)을 도시 또는 국가(상위수준)로 대체
•
예) 숫자(하위수준)를 어린이, 성인, 노인(상위수준)으로 매핑
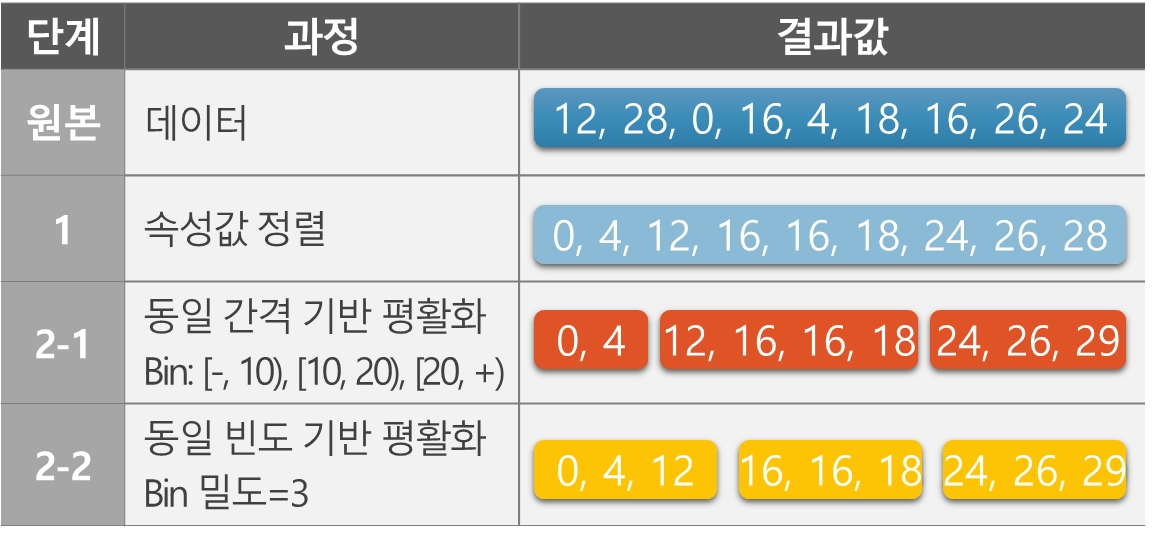
Binning (평활화)
이웃값을 기반으로 저장된 데이터를 여러 버킷(bin)으로 나누고, 각 세그먼트의 데이터를 특정 값(예: 평균, 경계값 등)으로 바꾸는 방법
평활화 예시
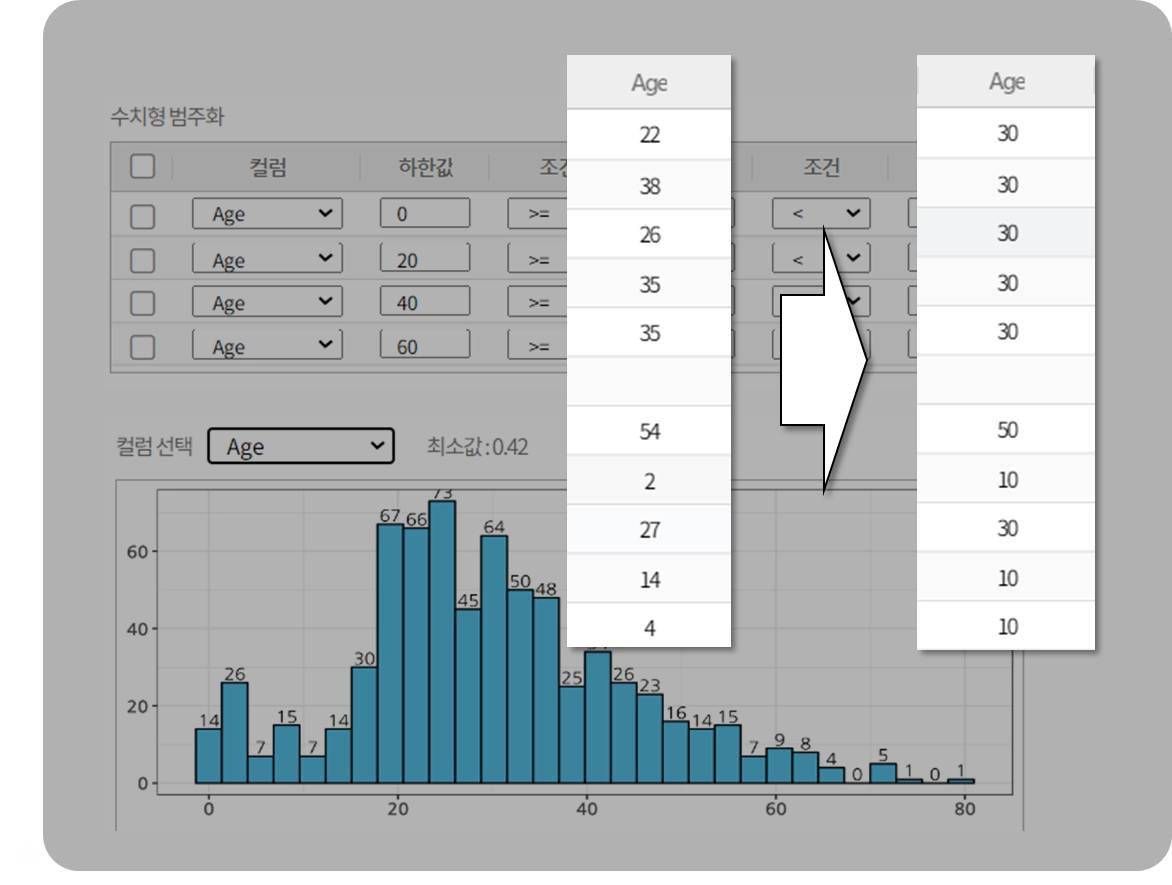
Age 컬럼의 평활화
문자열 파싱 or 문자열 조합
Building-Up and Breaking-Down Features
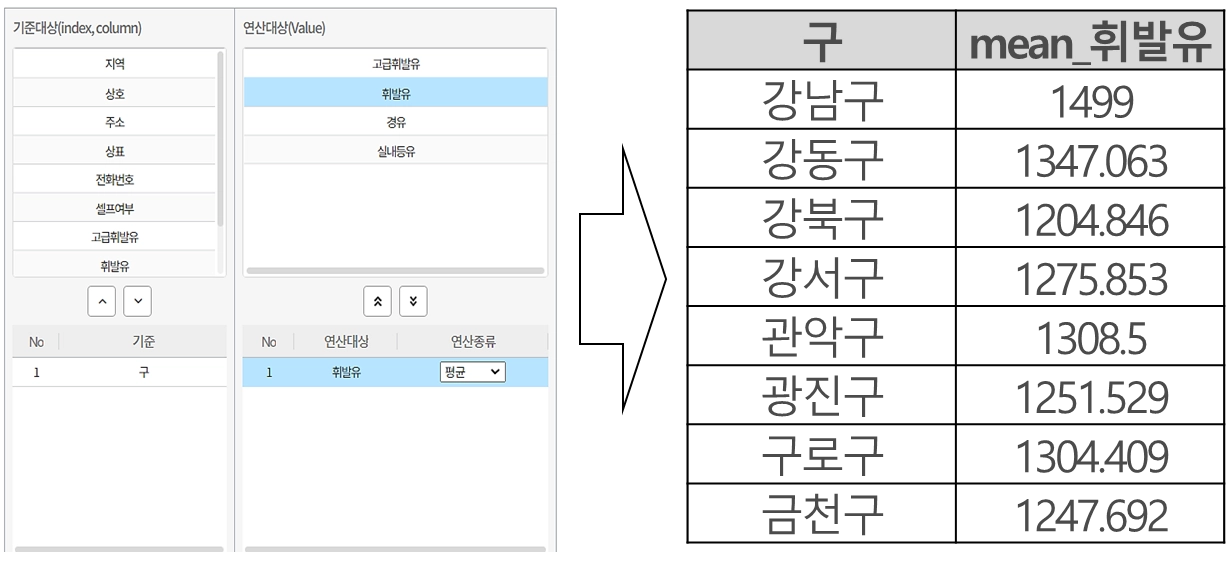
그룹화(Group Transforms)
그룹핑하여 정보의 대표값(예 : 평균)으로 값을 반영
정규화(Normalization)
•
데이터 값의 범위를 변환(Rescaling)시켜 학습결과가 과적합 될 가능성을 낮추는 방법
•
각 샘플 값에 대해 동일한 가중치를 적용하여 특정 샘플에 쏠림없이 데이터를 이해하는 작업
정규화의 필요성
•
측정 단위의 영향
◦
키 : 인치, 미터
◦
체중 : 파운드, 킬로그램
•
속성을 더 작은 단위로 표현하면 해당 속성의 범위가 넓어져 더 큰 '가중치'(또는 효과)를 줄 수 있음
•
측정 단위 선택에 의존하지 않도록 데이터를 변환해야 함
•
[0.0,1.0] 또는 [-1, 1]과 같이 공통 범위 내에 있도록 데이터를 변환
정규화의 효과
•
신경망, 최근접 이웃 분류, 클러스터링과 같은 거리 측정에 매우 유용
•
신경망 역전파 알고리즘을 사용하는 경우 모든 속성의 입력 값을 정규화하면 학습 속도가 빨라짐
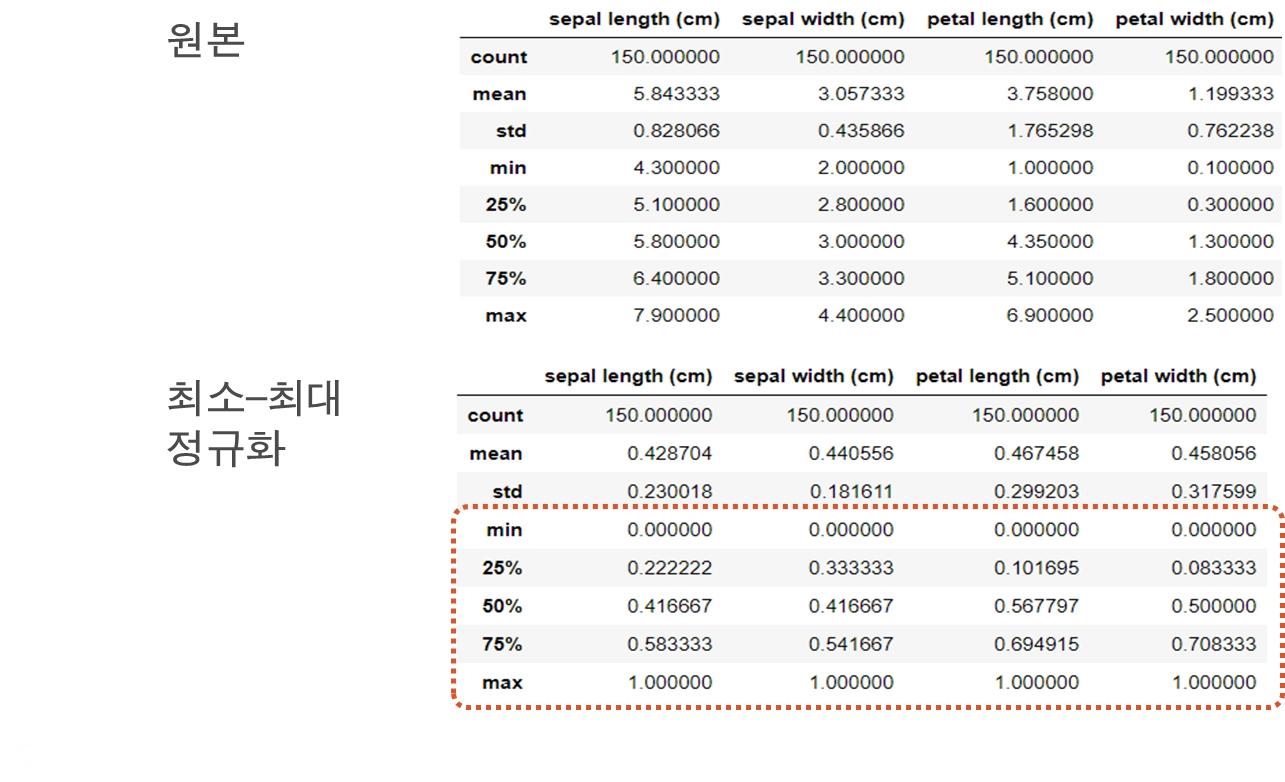
최소-최대 정규화(Min-Max Scaling)
•
원본 데이터에 대해 선형 변환을 수행
•
원래 데이터 값 간의 관계를 유지함
•
min(X)와 max(X) : 속성 X 의 최소값과 최대값
•
정규화 후 신규 입력 데이터가 X 의 원래 데이터 범위를 벗어나면 "범위 벗어남" 오류가 발생
[예시]
“소득” 속성의 최소값과 최대값이 각각 $10,000 및 $90,000일 때, 최소-최대 정규화를 사용하여 값을 [0.0, 1.0] 범위로 변환
소득 $70,000 의 정규화 결과
MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(df)
scaled_array = scaler.transform(df)
scaled_df = pd.DataFrame(data=scaled_array, columns=iris.feature_names)
scaled_df.describe()
Python
복사
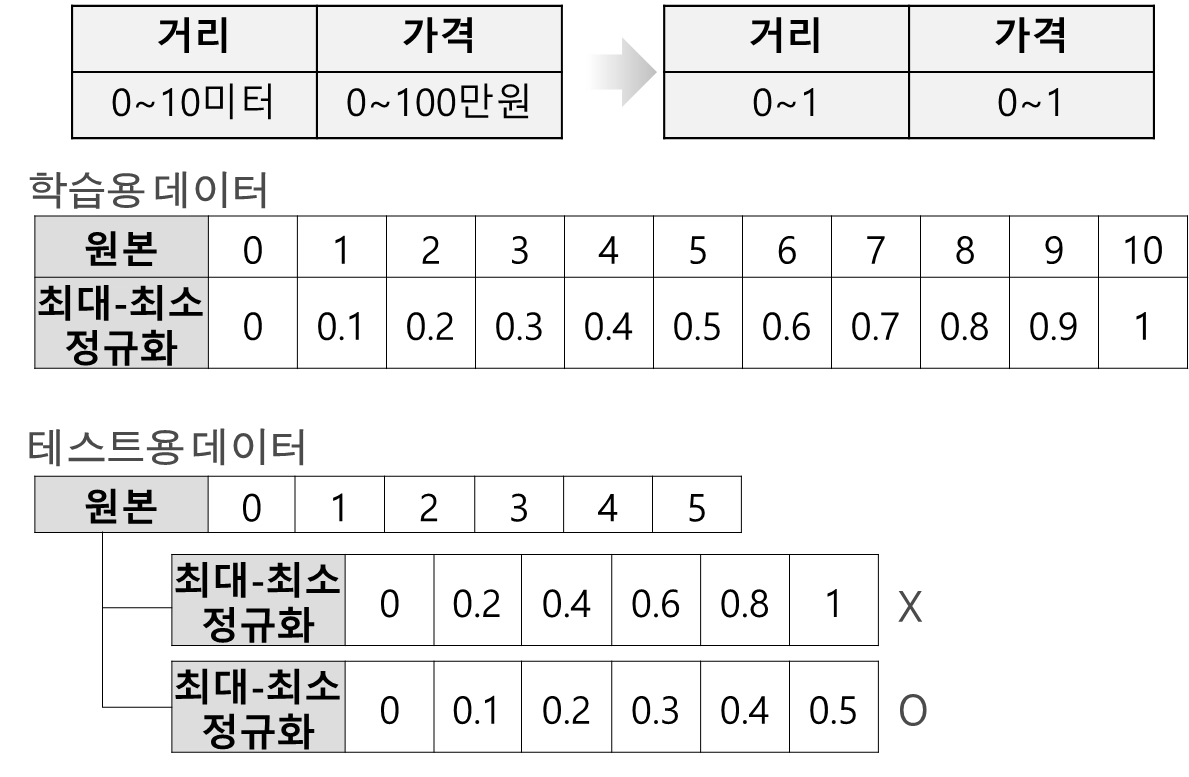
[예시] : 학습용 데이터와 테스트용 데이터
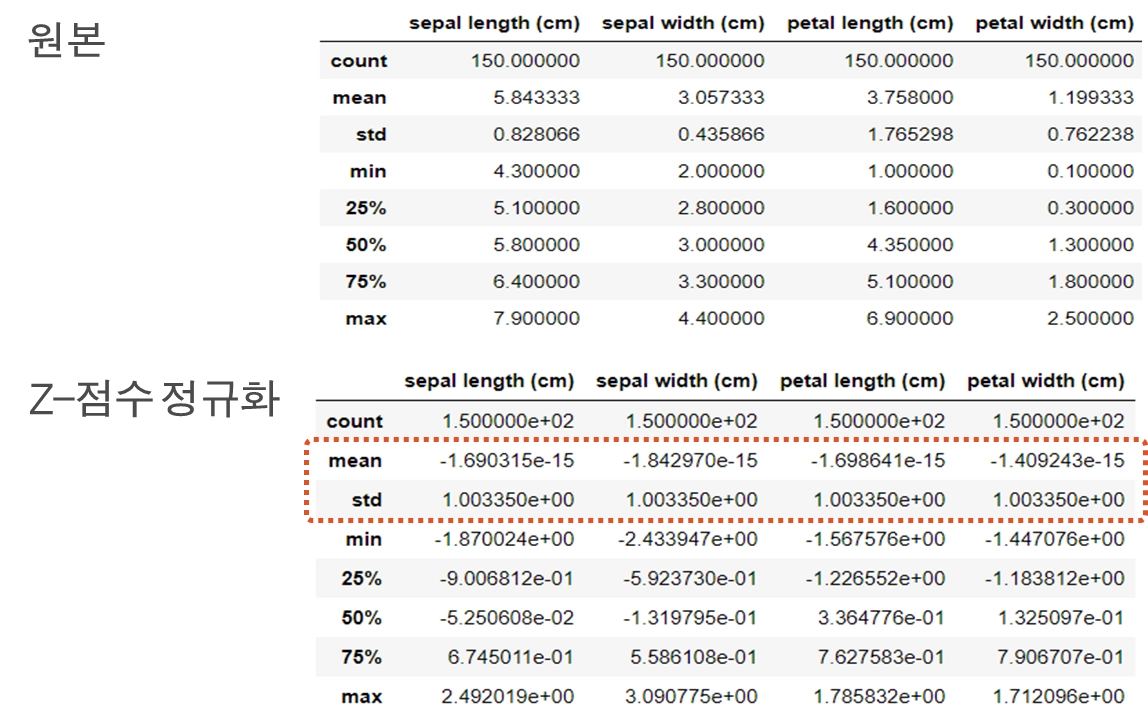
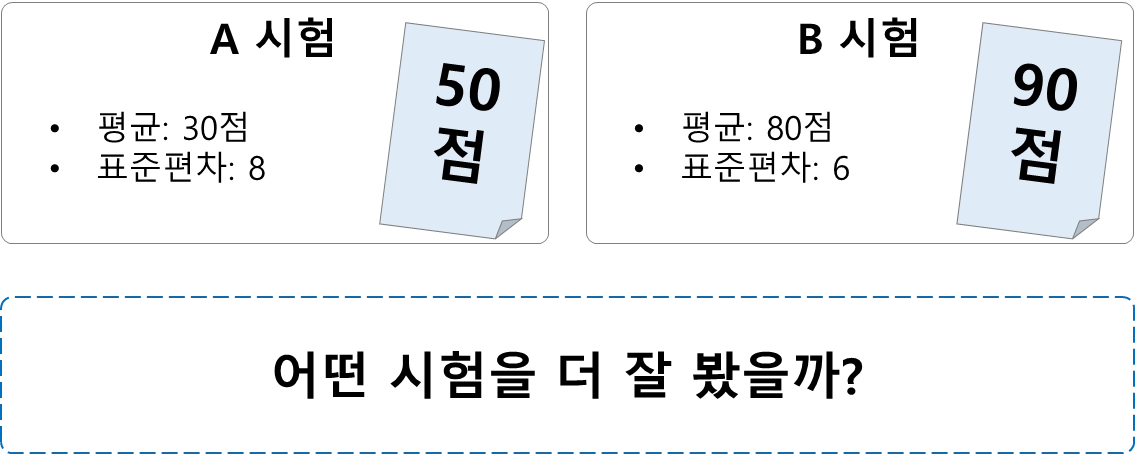
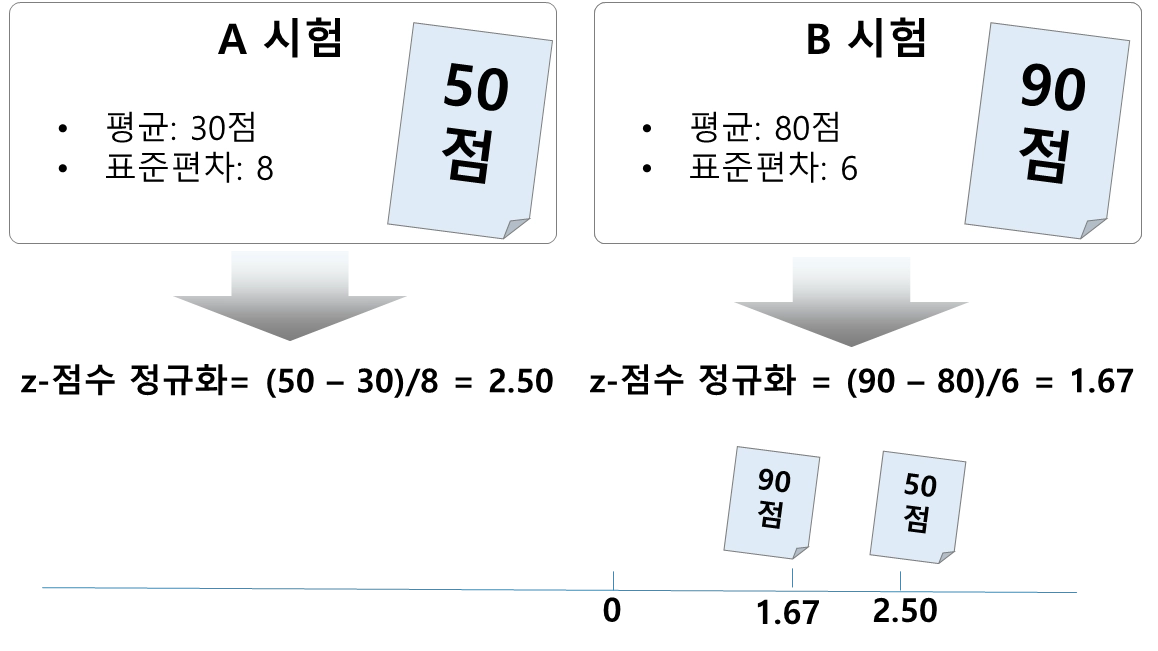
Z-점수(Z-score) 정규화
•
평균 및 표준편차를 사용하여 속성값을 정규화
•
개별 피처를 평균이 0, 분산이 1인 값으로 변환
•
SVM, 선형회귀, 로지스틱 회귀에서는 반드시 정규화 진행 필요
•
이상 값이 있거나 속성 X 의 실제 최소값과 최대값을 알 수 없는 경우에 유용
[예시]
”소득” 속성의 평균과 표준편차가 각각 $50,000 및 $10,000일 때, z-점수 정규화를 사용하여 값을 평균, 표준편차를 고려하여 변환
소득 $70,000 의 정규화 결과
StandardScaler
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(df)
scaled_array = scaler.transform(df)
scaled_df = pd.DataFrame(data=scaled_array, columns=iris.feature_names)
scaled_df.describe()
Python
복사
•
표준화(Standardization) 필요성
◦
표준화를 통해 단위가 다른 데이터들을 비교 할 수 있음
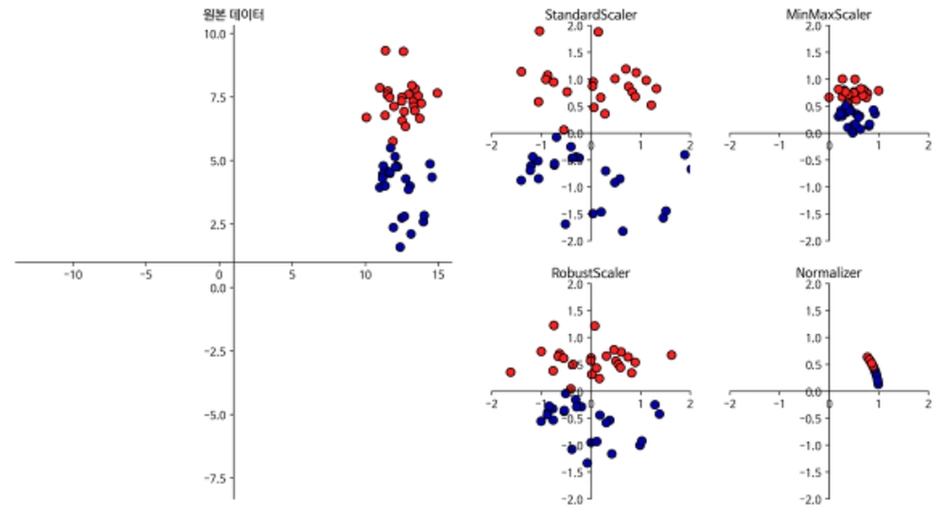
다양한 스케일링 기법
변환법 | 설명 | 특징 |
StandardScaler | - 평균 0, 분산 1로 변경
- 모든 특성이 같은 크기를 가지게 한다 | - 최소값과 최대값 크기를 제한하지는 않음 |
RobustScaler | - 특성들이 같은 스케일을 갖게 됨 (Standscaler 와 비슷) | - 평균과 분산 대신 중간 값(median) 와 사분위값(quantile) 사용
- 이상치 영향 받지 않음 |
MinMaxScaler | - 모든 특성이 0과 1 사이에 위치 | - 2차원 데이터 셋의 경우에는 x 축의 0과 1 , y축 0과 1사이에 값이 배치 |
Normalizer | - 특성 벡터의 유클리드안 길이가 1이 되도록 데이터 포인트를 조정 | - 지름이 1인 원에(3차원에서는 구)에 데이터 포인트를 투영 → 데이터 포인트가 다른 비율로(길이에 비례) 스케일이 조정
- 이러한 정규화는 특성 벡터의 길이는 상관없고 데이터 방향(도는 각도)만이 중요할 때 많이 사용 |