🕌

용어정리

주요 개념

Perceptron Hidden layer MLP Back propagation Feedforward Neural Network Activation Function Loss Function

•

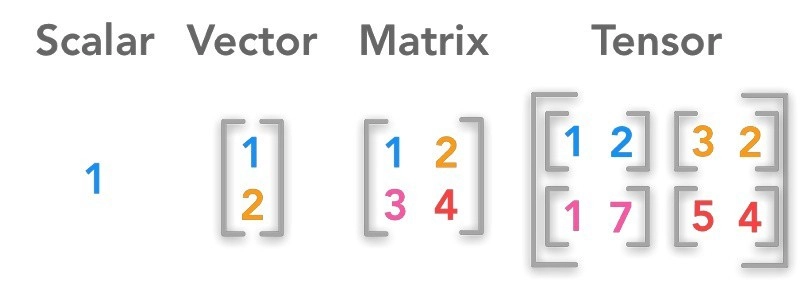
벡터, 행렬,  텐서는 모두 수학 및 데이터 과학에서 사용하는 데이터 구조

벡터 (Vector):

•

1차원 배열로, 숫자들의 순서가 있는 리스트

•

주로 물리학과 수학에서 방향과 크기를 가진 물리량을 표현하는 데 사용

[a_1,a_2,a_3,...,a_n]

행렬(Matrix):

•

 2차원 배열로, 수나 다른 수학적 객체들이 행과 열로 배열된 구조

•

행과 열이 있는 2차원 구조

\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}

텐서 (Tensor):

•

텐서는 다차원 배열의 일반화된 개념으로, 0차원 (스칼라), 1차원 (벡터), 2차원 (행렬) 및 그 이상의 차원을 가질 수 있음

•

머신러닝과 딥러닝에서는 데이터와 가중치를 표현하는 데 사용

\mathbf{T} = \begin{bmatrix} \begin{bmatrix} t_{111} & t_{112} \\ t_{121} & t_{122} \\ t_{131} & t_{132} \\ t_{141} & t_{142} \end{bmatrix}, \begin{bmatrix} t_{211} & t_{212} \\ t_{221} & t_{222} \\ t_{231} & t_{232} \\ t_{241} & t_{242} \end{bmatrix}, \begin{bmatrix} t_{311} & t_{312} \\ t_{321} & t_{322} \\ t_{331} & t_{332} \\ t_{341} & t_{342} \end{bmatrix} \end{bmatrix}